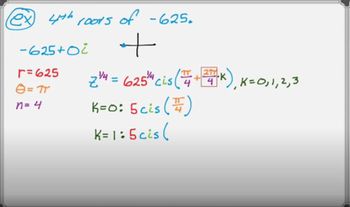In Exercises 69–76, find all the complex roots. Write roots in rectangular form. If necessary, round to the nearest tenth. The complex fourth roots of 81 (cos 4π/3 + i sin 4π/3)

Key Concepts

Complex Numbers

Complex numbers are numbers that have a real part and an imaginary part, expressed in the form a + bi, where 'a' is the real part and 'b' is the imaginary part. They are essential in various fields of mathematics and engineering, allowing for the solution of equations that do not have real solutions. Understanding how to manipulate and represent complex numbers is crucial for finding roots and performing operations in the complex plane.

De Moivre's Theorem

De Moivre's Theorem states that for any complex number in polar form r(cos θ + i sin θ), the nth roots can be found using the formula r^(1/n)(cos(θ/n + 2kπ/n) + i sin(θ/n + 2kπ/n)), where k is an integer from 0 to n-1. This theorem simplifies the process of finding roots of complex numbers by converting them into polar coordinates, making it easier to apply trigonometric identities.

Polar and Rectangular Forms

Complex numbers can be represented in two forms: rectangular form (a + bi) and polar form (r(cos θ + i sin θ)). The rectangular form is useful for addition and subtraction, while the polar form is advantageous for multiplication, division, and finding roots. Converting between these forms is a key skill in complex analysis, especially when dealing with roots and trigonometric functions.