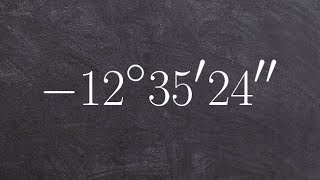Perform each calculation. See Example 3. 90° ― 51° 28'

Verified step by step guidance

1. Convert the angle 51° 28' into decimal degrees. To do this, divide the minutes by 60 since there are 60 minutes in a degree.
2. Subtract the decimal degree equivalent of 51° 28' from 90°.
3. If necessary, convert the result back into degrees and minutes by taking the decimal part and multiplying by 60 to get the minutes.
4. Ensure the final answer is in the correct format, either in decimal degrees or degrees and minutes.
5. Double-check the subtraction to ensure accuracy in the conversion and calculation steps.

Key Concepts

Angle Measurement

Angles can be measured in degrees and minutes, where 1 degree equals 60 minutes. In this context, the angle is expressed as 51 degrees and 28 minutes, which is a common way to represent angles in trigonometry. Understanding how to convert between degrees and minutes is essential for accurate calculations.

Subtraction of Angles

Subtracting angles involves taking one angle measurement away from another. When performing this operation, it is important to align the degrees and minutes correctly. If the minutes of the angle being subtracted exceed those of the angle from which it is being subtracted, borrowing from the degrees may be necessary.

Complementary Angles

Two angles are complementary if their sum equals 90 degrees. In this problem, the calculation involves finding the complement of 51 degrees and 28 minutes. Recognizing the relationship between complementary angles is crucial for solving problems that involve angle subtraction and understanding their geometric implications.