Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
0. Review of College Algebra
Basics of Graphing
Problem 61
Textbook Question
In the following exercises, (a) find the center-radius form of the equation of each circle described, and (b) graph it. See Examples 5 and 6. center (√2, √2), radius √2
 Verified step by step guidance
Verified step by step guidance1
Identify the center of the circle as \((\sqrt{2}, \sqrt{2})\) and the radius as \(\sqrt{2}\).
Recall the center-radius form of a circle's equation: \((x - h)^2 + (y - k)^2 = r^2\), where \((h, k)\) is the center and \(r\) is the radius.
Substitute the center \((h, k) = (\sqrt{2}, \sqrt{2})\) and the radius \(r = \sqrt{2}\) into the equation.
The equation becomes \((x - \sqrt{2})^2 + (y - \sqrt{2})^2 = (\sqrt{2})^2\).
Simplify the equation to \((x - \sqrt{2})^2 + (y - \sqrt{2})^2 = 2\).
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Center-Radius Form of a Circle
The center-radius form of a circle's equation is expressed as (x - h)² + (y - k)² = r², where (h, k) is the center of the circle and r is the radius. This format allows for easy identification of the circle's center and radius, facilitating both graphing and analysis of the circle's properties.
Recommended video:

Introduction to the Unit Circle
Graphing a Circle
Graphing a circle involves plotting its center on a coordinate plane and using the radius to determine the points that lie on the circle. From the center, you can move r units in all directions (up, down, left, right) to find key points, which can then be connected to form the circular shape.
Recommended video:

Introduction to the Unit Circle
Distance Formula
The distance formula, derived from the Pythagorean theorem, calculates the distance between two points in a plane. It is given by d = √((x₂ - x₁)² + (y₂ - y₁)²). This concept is essential for understanding how far points are from the center of the circle, which helps in verifying if points lie on the circle.
Recommended video:

Quadratic Formula

 5:1m
5:1mWatch next
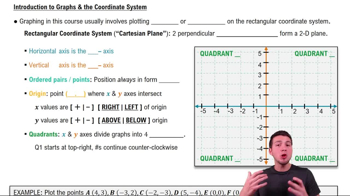
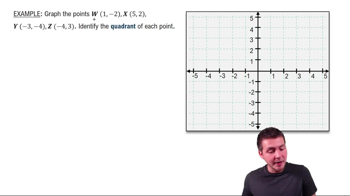
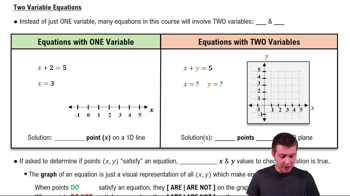
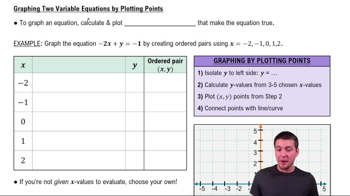
Master Introduction to Graphs & the Coordinate System with a bite sized video explanation from Patrick Ford
Start learning