Concept Check The two methods of expressing bearing can be interpreted using a rectangular coordinate system. Suppose that an observer for a radar station is located at the origin of a coordinate system. Find the bearing of an airplane located at each point. Express the bearing using both methods. (2, 2)

Verified step by step guidance

1. <Step 1: Understand the concept of bearing. Bearing is a way of describing direction, often used in navigation. It can be expressed in two ways: as a compass bearing (using degrees from North) or as a quadrant bearing (using directions like NE, SE, etc.).>
2. <Step 2: Identify the coordinates of the airplane. The airplane is located at the point (2, 2) in the coordinate system.>
3. <Step 3: Calculate the angle from the positive x-axis. Since the point (2, 2) is in the first quadrant, use the arctangent function to find the angle: \( \theta = \tan^{-1}\left(\frac{y}{x}\right) = \tan^{-1}\left(\frac{2}{2}\right) \).>
4. <Step 4: Convert the angle to a compass bearing. Since the angle is measured from the positive x-axis (East), convert it to a compass bearing by subtracting it from 90 degrees (since North is 90 degrees from East).>
5. <Step 5: Express the bearing in both methods. The compass bearing is the angle from North, and the quadrant bearing is expressed as NE, SE, etc. In this case, the point (2, 2) is in the NE direction.>

Key Concepts

Bearing

Bearing is a method of expressing direction relative to a reference direction, typically north. It is measured in degrees clockwise from the north direction, ranging from 0° to 360°. For example, a bearing of 90° indicates an eastward direction, while 180° points south. Understanding how to calculate and interpret bearings is essential for navigation and positioning in a coordinate system.

Rectangular Coordinate System

A rectangular coordinate system, also known as the Cartesian coordinate system, uses two perpendicular axes (x and y) to define the position of points in a plane. The origin (0,0) is where the axes intersect. Each point is represented by an ordered pair (x, y), which indicates its horizontal and vertical distances from the origin. This system is crucial for visualizing and calculating bearings in relation to specific coordinates.

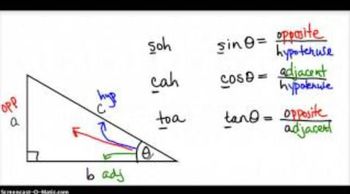
Trigonometric Functions

Trigonometric functions, such as sine, cosine, and tangent, relate the angles of a triangle to the lengths of its sides. In the context of bearings, these functions can be used to determine the angle of elevation or depression and to convert between rectangular coordinates and polar coordinates. For example, the tangent function can help find the angle of a point in relation to the origin, which is essential for calculating the bearing of the airplane.