Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
4. Graphing Trigonometric Functions
Graphs of the Sine and Cosine Functions
Problem 60
Textbook Question
Textbook QuestionIn Exercises 53–60, use a vertical shift to graph one period of the function. y = −3 sin 2πx + 2
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
10mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Sine Function
The sine function is a periodic function that describes the relationship between an angle and the ratio of the opposite side to the hypotenuse in a right triangle. It oscillates between -1 and 1, and its graph is a smooth wave. In the context of the given function, the sine function is modified by amplitude and vertical shifts.
Recommended video:

Graph of Sine and Cosine Function
Amplitude
Amplitude refers to the maximum distance the graph of a periodic function reaches from its midline. In the function y = -3 sin 2πx + 2, the amplitude is 3, indicating that the graph will reach 3 units above and below its midline. The negative sign indicates that the graph is reflected over the midline.
Recommended video:
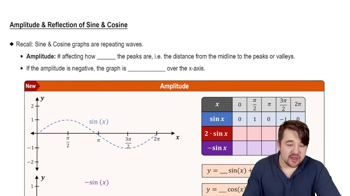
Amplitude and Reflection of Sine and Cosine
Vertical Shift
A vertical shift occurs when a constant is added to or subtracted from a function, moving the entire graph up or down. In the function y = -3 sin 2πx + 2, the '+2' indicates a vertical shift of 2 units upward. This shift affects the midline of the sine wave, changing the center of oscillation from y=0 to y=2.
Recommended video:
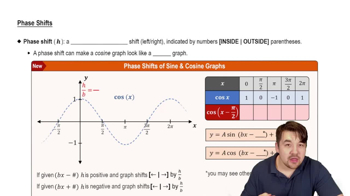
Phase Shifts

 5:53m
5:53mWatch next
Master Graph of Sine and Cosine Function with a bite sized video explanation from Nick Kaneko
Start learningRelated Videos
Related Practice