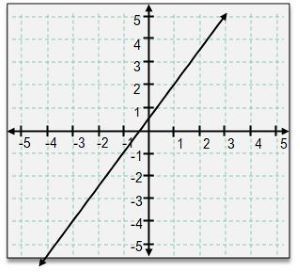
Understanding the concept of slope is essential when analyzing linear equations. The slope, denoted as m, quantifies the steepness of a line and can be calculated using any two points on that line. Mathematically, the slope is defined as the change in the y values divided by the change in the x values, expressed with the formula:
\[ m = \frac{y_2 - y_1}{x_2 - x_1} \]
In this equation, (x1, y1) and (x2, y2) represent two distinct points on the line. To simplify notation, the Greek letter delta (Δ) is often used, leading to the shorthand:
\[ m = \frac{\Delta y}{\Delta x} \]
Here, Δy represents the vertical change (rise) and Δx represents the horizontal change (run). For example, if you have two points, (1, 2) and (2, 4), you can calculate the slope as follows:
1. Identify the points: (x1, y1) = (1, 2) and (x2, y2) = (2, 4).
2. Substitute into the slope formula:
\[ m = \frac{4 - 2}{2 - 1} = \frac{2}{1} = 2 \]
This indicates that for every unit you move horizontally (run), the line rises by 2 units (rise).
When analyzing different lines, it's important to note that a steeper line will have a higher slope value. For instance, if another line has points (4, -1) and (5, 4), the slope can be calculated similarly:
1. Identify the points: (x1, y1) = (4, -1) and (x2, y2) = (5, 4).
2. Substitute into the slope formula:
\[ m = \frac{4 - (-1)}{5 - 4} = \frac{5}{1} = 5 \]
This means that for every unit you move horizontally, the line rises by 5 units, indicating a steeper incline compared to the previous line.
It’s also worth noting that the order of the points does not affect the slope calculation. For example, if you switch the points in the first example, you would still arrive at the same slope value, although the signs may change:
\[ m = \frac{2 - 4}{1 - 2} = \frac{-2}{-1} = 2 \]
In conclusion, the slope is a fundamental concept in understanding linear relationships, where a lower slope indicates a gentler incline and a higher slope indicates a steeper incline. Mastering the calculation of slope will enhance your ability to interpret and analyze linear graphs effectively.