Graphs of Secant and Cosecant Functions - Online Tutor, Practice Problems & Exam Prep

Understanding the cosecant and secant functions involves recognizing them as the reciprocals of sine and cosine, respectively. Their graphs can be derived from sine and cosine graphs, with asymptotes at points where sine or cosine equals zero. The cosecant graph features peaks and valleys, resembling a smiley and frowny face pattern, while the secant graph has similar characteristics but with different asymptote locations. Transformations applicable to sine and cosine also apply to cosecant and secant, allowing for effective graphing of functions like y = cosecant(2x), where the period is π.

Graphs of Secant and Cosecant Functions

Hey everyone. So up to this point, we've spent a lot of time dealing with the sine and cosine functions, and we've discussed their graphs and different ways that the graphs can be transformed, like being stretched or shifted in some kind of way. Well, in this video, we're going to learn that we can graph more trigonometric functions such as the secant and cosecant. And this might sound a little bit scary at first, but don't sweat it because it turns out we can actually use the graphs that we learned about for sine and cosine to graph the cosecant and secant. So without further ado, let's get right into this.

Now recall that the cosecant and secant are reciprocals, they're reciprocal identities for the sine and cosine. So cosecant is 1sin and secant is 1cos, and you can use these relationships to figure out what their graphs look like. So, I'm just going to jump right into the cosecant graph. And if I go ahead and take the reciprocal for all these outputs that I see, the reciprocal of 1 is just 1. The reciprocal of negative one is negative one because 1 divided by negative one would be negative one, and then the reciprocal of 1 is just 1 there. So that means at an x-value of π2, we'll have 1. For 3π2, we're going to have negative 1. And then for 5π2, we're going to have 1 again.

Now I'm also going to need to take the reciprocal of these values, but notice that all of these values are 0. And if I take the reciprocal of 0, that's just going to be 10. But this is actually a problem, because recall that in math, it's a fundamental rule that we cannot divide by 0. So what does this mean? Well, that means that every place we see 0 for our sine value, our cosecant is going to be undefined. And for undefined values, what we're basically saying in this instance is that they're approaching infinity. And since infinity is not a number, we can't define it. So what we can do is we can take asymptotes and draw them where we see the sine function reach 0. So, we're going to have an asymptote at an x-value of 0. We'll have another asymptote at an x-value of π, and we'll have another asymptote at an x-value of 2π.

Now from here, I need to figure out how the rest of the graph is going to behave. And the way that I can do this is by simply observing how the sine function behaves. Notice how the sine function gets smaller and smaller as we go to the left and as we go to the right. And what happens if you take the reciprocal of a number that gets smaller and smaller? Well, the whole fraction is going to get bigger and bigger. And because of this, our cosecant function is going to blow up as we go to the left and to the right. So we in essence end up with this kind of smiley face thing happening right here, and it turns out that this logic stays true for all the other points. So notice how we end up with these smiley and frowny faces where we have the peaks and valleys respectively.

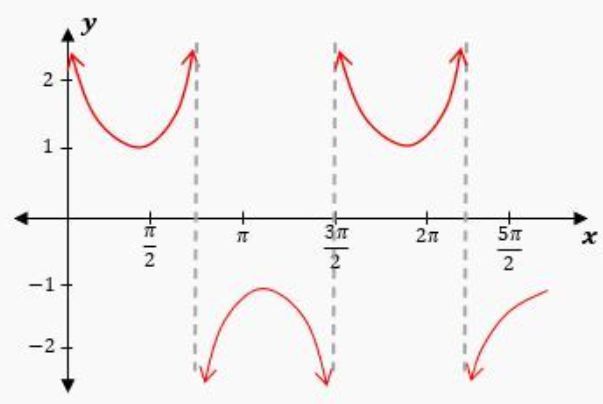
Now let's also take a look and see how the secant function behaves. Well, I can use the same logic by taking the reciprocal of all these values for the cosine. The reciprocal of 1 is 1, and then we have the reciprocal of negative one and the reciprocal of 1. So going to our graph, our points are going to be at 1 at the peak there, at negative one for the valley at an x-value of π, and then at another peak, we're going to have 1 as well. Now because secant is a reciprocal of the cosine, all the places that we see 0 for the cosine are going to be undefined for the secant. So when doing this we can actually draw asymptotes at all these undefined values. So at an x-value of π2, we're going to have an asymptote. At 3π2, we're going to have another asymptote. And then at 5π2, we're going to have another asymptote. Now just like we saw with the cosecant, this graph is a reciprocal of the cosine. So just like with the cosecant graph, we're going to see these kind of smiley faces and frowny faces where the peaks and valleys are. So notice how these two graphs end up looking very similar. The really key difference between these two graphs is where the asymptotes are located. Because notice for the cosecant, we ended up with asymptotes at 0, π, 2π, basically just integer multiples of π. And for the secant, we ended up with asymptotes at π2, 3π2, 5π2, or basically just odd multiples of π2.

Now something that's really nice about the cosecant and secant graphs is it turns out that you can use all the same transformation rules that you use for the sine and cosine. So all the stretches and shifts for the cosecant and secant function that we learned about are going to hold true. And to see this, let's actually take a look at an example.

In this example, we are asked to graph the function y = 1sin(2x). You may be a little bit curious where we need to start with this example or how we could even do this, but what I personally like to do when dealing with these types of problems is to first figure out what I know and then build off of that. Now one of the things I know about the cosecant is I know the cosecant is a reciprocal of the sine. And so what I'm actually going to do is first find the graph of y = sin(2x). Now this is not the graph that we're looking for, but this will give me an idea as to what the cosecant is going to look like since I know their relationship. So recall that for sine of 2x, well, we first need to figure out what the period is. And the period for a sine or cosine graph is 2πb. Now the b value that we have in front is 2. So we're going to have 2π2, where the twos will cancel and give us π. So that means that we're going to have a sine graph that has its period at π. So what that means is that our sine graph will start at the origin, and we're going to reach a peak right about there, then we__*/

Below is a graph of the function $y=\sec\left(bx-\pi\right)$. Determine the value of b.

• A. $b=2$
• B. $b=4$
• C. $b=\frac{\pi}{2}$
• D. $b=\pi$

Below is a graph of the function $y=\csc\left(bx\right)$. Determine the value of b.

• A. $b=\frac12$
• B. $b=3$
• C. $b=\frac43$
• D. $b=\frac{3\pi}{4}$

Here’s what students ask on this topic:

What are the key differences between the graphs of secant and cosecant functions?

The key differences between the graphs of secant and cosecant functions lie in the locations of their asymptotes and their relationship to the sine and cosine functions. The secant function, being the reciprocal of the cosine function, has asymptotes where the cosine function equals zero, which are at odd multiples of π/2 (e.g., π/2, 3π/2). The cosecant function, being the reciprocal of the sine function, has asymptotes where the sine function equals zero, which are at integer multiples of π (e.g., 0, π, 2π). Both graphs feature peaks and valleys, resembling smiley and frowny faces, but their asymptote locations differ due to their respective reciprocal relationships.

How do you graph the secant function using the cosine function?

To graph the secant function using the cosine function, follow these steps: First, graph the cosine function. Identify the points where the cosine function equals zero, as these will be the locations of the vertical asymptotes for the secant function. These points occur at odd multiples of π/2 (e.g., π/2, 3π/2). Next, take the reciprocal of the cosine values at other points to plot the secant function. The secant function will have peaks and valleys at the same points where the cosine function has its maximum and minimum values. Finally, draw the secant function, ensuring it approaches the asymptotes and forms the characteristic smiley and frowny faces between them.

What are the asymptotes of the cosecant function?

The asymptotes of the cosecant function occur at the points where the sine function equals zero. These points are at integer multiples of π (e.g., 0, π, 2π). Since the cosecant function is the reciprocal of the sine function, it becomes undefined at these points, resulting in vertical asymptotes. When graphing the cosecant function, you will draw vertical lines at these x-values to represent the asymptotes, and the function will approach these lines but never touch them.

How do transformations affect the graphs of secant and cosecant functions?

Transformations affect the graphs of secant and cosecant functions in the same way they affect sine and cosine functions. Horizontal shifts, vertical shifts, stretches, and compressions can all be applied. For example, if you have y = csc(2x), the period of the function is halved, resulting in more frequent peaks and valleys. Vertical shifts move the entire graph up or down, while horizontal shifts move it left or right. Amplitude changes affect the height of the peaks and valleys. Understanding these transformations helps in accurately graphing secant and cosecant functions.

How do you determine the period of the cosecant function?

To determine the period of the cosecant function, you first need to identify the period of its reciprocal function, the sine function. The period of the sine function is given by the formula 2π/b, where b is the coefficient of x in the argument of the sine function. For example, in y = csc(2x), the period of the sine function is 2π/2 = π. Since the cosecant function is the reciprocal of the sine function, it shares the same period. Therefore, the period of the cosecant function is also π in this case.