Write an equation of a line that passes through the point (3,−4)\left(3,-4\right)(3,−4) and is parallel to the line x+2y+18=0x+2y+18=0x+2y+18=0.

y + 4 = − 1 2 ( x − 3 ) y+4=-\frac12\left(x-3\right) y + 4 = − 2 1 ( x − 3 )

Write an equation of a line that passes through the point ( 3 , − 4 ) \left(3,-4\right) ( 3 , − 4 ) and is parallel to the line x + 2 y + 18 = 0 x+2y+18=0 x + 2 y + 18 = 0 .

Welcome back, everyone. In this problem, we're gonna write an equation of a line that passes through a point 3 comma negative 4. We're also told that this line is parallel to a line that's given to us, and this line is x plus 2y+18 equals 0. So this is a line that's in standard form. So let's get started. Now remember, these types of problems really just use the words parallel and perpendicular to give you keywords or clues about the slope that they want. And notice how, also, this problem doesn't really tell us what sort of form that they want our equation in. But because they're giving us information about the point and and we're supposed to find information about the slope, then it's the best sort of getting the most direct to write the equation of alarm of our line in point slope form. Really, you can convert these to standard form or even, slope intercept form, but it's gonna be easiest to write our specific one in point slope form. So let's go ahead and do that. So notice how so remember how the equation goes. It's gonna be y minus y one equals m parenthesis x minus x one. Now remember, there's 3 things that we need for this equation. We need the coordinates x one and y one, and we also need the slope. So we need 3 of those numbers to plug in. That's gonna be the equation of our line. Now remember, in these types of problems, whenever they're telling you that it passes through some kind of a point like 3 comma negative 4, really, what they're doing is they're actually just giving you what x one and y one are. That's really all they're doing. So we can just take these numbers here, like 3 negative 4, and we'll just pop them into our equation. And that's already gonna be most of our variables solved for. So y one in this situation is gonna be minus 4, so just remember the negative sign there, equals m, and we don't know what that is, x minus x 1, and then in this case, that's just gonna be 3. Alright? So we're almost actually done. All we really just need to do is find the slope of the line, and then we're gonna be done here. So how do we figure out the slope? Well, we're gonna have to do a little bit more work here because remember, now instead of points to calculate the slope, we're really just told that it's parallel to some line that it's giving it that that that's given to us, and that's this line over here. So remember to get m, what parallel means is that the slopes are the same. So in other words, m 2 is equal to m 1. Right? The slopes are the same. Another way of sort of writing this is that the m targets, the thing that we're trying to look for, the slope of the line that we're trying to write, is equal to the slope of the line that's given to us. So what's the slope of the line that's given to us? Well, we actually can't tell because this thing is written in standard form. It's x plus 2 y plus 18 equals 0. Notice how this is not equal to y equals mx plus b, so we can't sort of extract the m out. However, what we have seen is that we can take a line in standard form, and we can rewrite it in slope intercept form. So really, all we have to do is take this x plus 2 y plus 18 equals 0, and all we have to do in this case is just solve for y. So when you solve for y and you isolate it to the left side, you're gonna turn it into y equals mx plus b, and then we can figure out what the slope of this line is. Once we figure out what the slope of this line is, that's the slope of our line that we're trying to write an equation for. Okay? So let's get started. All we have to do is just move this 18 to the other side and sort of isolate y, so we're gonna subtract 18 from both sides. And then I also have to bring the x over to the left side as well by subtracting x from both sides. When I'm do when I do this, I end up with 2 y equals negative x minus 18. And now what I do is I just divide by 2 from each side. So I divide by 2 from everything in the equation, and that'll go away. And then, finally, what I'm just left with is y equals negative one half x minus 9. So this is the equation, x plus 2 y plus 18 equals 0, just written in slope intercept form. And remember, what we can see here is that it's because this is in y equals mx plus b, then really what happens is the m is equal to negative one half. So in other words, the m that's given to us is negative one half. And remember what we said, the m of our target variable or, sorry, the slope of the line that we're trying to find is gonna have the same exact m. So in other words, m targets, the one that I'm looking for here, is also gonna be equal to negative one half. So negative one half over here. So, really, we're just gonna put all this stuff together, and this is gonna be y+4 equals negative one half parenthesis x minus 3. Now this is the equation of the line that you're specifically looking for. It has the same slope as this equation over here, and it also passes through this coordinate 3 comma negative 4. You could take this equation and you could rewrite it in slope intercept form, or you can even write it in standard form if you want, but I'm just gonna leave it like that. So, hopefully, that made sense. Thanks for watching.

Write an equation of a line that passes through the point ( 3 , − 4 ) \left(3,-4\right) ( 3 , − 4 ) and is parallel to the line x + 2 y + 18 = 0 x+2y+18=0 x + 2 y + 18 = 0 .

y + 4 = − 1 2 ( x − 3 ) y+4=-\frac12\left(x-3\right) y + 4 = − 2 1 ( x − 3 )

y + 4 = − 2 ( x − 3 ) y+4=-2\left(x-3\right) y + 4 = − 2 ( x − 3 )

y = − 1 2 ( x − 3 ) y=-\frac12\left(x-3\right) y = − 2 1 ( x − 3 )

y − 3 = − 1 2 ( x + 4 ) y-3=-\frac12\left(x+4\right) y − 3 = − 2 1 ( x + 4 )

2. Graphs

Lines

Precalculus

2. Graphs

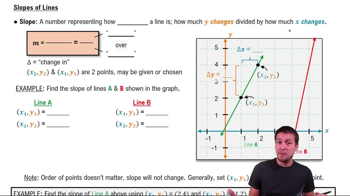
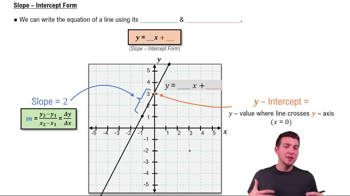
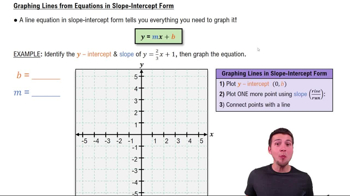
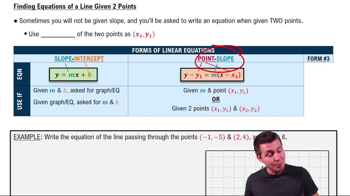
Lines

Struggling with Precalculus?

Join thousands of students who trust us to help them ace their exams!Watch the first video

Multiple Choice

Write an equation of a line that passes through the point $\left(3,-4\right)$ and is parallel to the line $x+2y+18=0$ .

$y+4=-\frac12\left(x-3\right)$

$y+4=-2\left(x-3\right)$

$y=-\frac12\left(x-3\right)$

$y-3=-\frac12\left(x+4\right)$

Verified step by step guidance

Identify the slope of the given line. The equation of the line is x + 2y + 18 = 0. Rewrite it in slope-intercept form (y = mx + b) to find the slope.

To convert x + 2y + 18 = 0 to slope-intercept form, solve for y: 2y = -x - 18, then y = -\frac{1}{2}x - 9. The slope (m) is -\frac{1}{2}.

Since parallel lines have the same slope, the line we are looking for will also have a slope of -\frac{1}{2}.

Use the point-slope form of a line equation, y - y_1 = m(x - x_1), where (x_1, y_1) is the point (3, -4) and m is the slope -\frac{1}{2}.

Substitute the point (3, -4) and the slope -\frac{1}{2} into the point-slope form: y + 4 = -\frac{1}{2}(x - 3). This is the equation of the line parallel to the given line and passing through the point (3, -4).

6:49m

Watch next

Master The Slope of a Line with a bite sized video explanation from Patrick

Start learning