Find the limit by creating a table of values. lim ⁡ x → 1 x 2 − 4 x − 2 \lim_{x\rarr1}\frac{x^2-4}{x-2} lim x → 1 x − 2 x 2 − 4

Here, we're asked to find the limit by creating a table of values. And the limit that we're asked to find here is the limit of x squared minus 4 over x+2 as x approaches 1. So since we're looking at x approaching 1 here for this limit, we wanna look at values that are getting really, really close to 1 from either side. So we're going to start with values that are actually less than 1 getting really, really close to it. And remember that you can sort of think of this as values kind of closing in on 1. So we want to think of values that are really, really close like 0.99 and getting even closer, 0.999. Now if I take these values and plug them into my function here, x squared minus 4 over x+2, starting with this 0.99, if I plug this value into my function, I'll have 0.99 squared minus 4 over 0.99 minus 2. Now actually working that algebra out, feel free to do this on your own and try it before you check back in with me. You can always plug this into your calculator as well, and you should get an answer here of 2.99. Now, if we do the same thing here for 0.999, you should get an answer of 2.999. Now here, we notice that these values are sort of closing in on 3, but let's check the other side too. So values that are kind of closing in on 1 coming in from that right side. Now I wanna think of values here like 1.001 and 1.01. And, again, just plugging these values into our function, like this 1.001, that's gonna give me 3 point 1. And then for this 1.01, that's going to give me a 3.01. Now here again, we see that these values are closing in on 3. So that tells us that our limit here of x squared minus 4 over x minus 2 as x approaches 1 is equal to 3. And that's our final answer. Free to let me know if you have any questions, but I'll see you in the next one.

22. Limits & Continuity

Introduction to Limits

Precalculus

22. Limits & Continuity

Introduction to Limits

Struggling with Precalculus?

Join thousands of students who trust us to help them ace their exams!Watch the first video

Multiple Choice

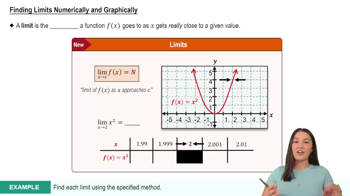
Find the limit by creating a table of values.
$\lim_{x\rarr1}\frac{x^2-4}{x-2}$

$0$

$3$

$-3$

$2$

Verified step by step guidance

Identify the function for which you need to find the limit: $ f(x) = \frac{x^2 - 4}{x - 2} $.

Notice that direct substitution of $ x = 1 $ into the function results in an indeterminate form $ \frac{0}{0} $. This suggests that the function may have a removable discontinuity at $ x = 1 $.

To resolve the indeterminate form, factor the numerator $ x^2 - 4 $ as $ (x - 2)(x + 2) $. The function can then be rewritten as $ \frac{(x - 2)(x + 2)}{x - 2} $.

Cancel the common factor $ x - 2 $ from the numerator and the denominator, simplifying the function to $ f(x) = x + 2 $ for $ x \neq 2 $.

Create a table of values approaching $ x = 1 $ from both sides (e.g., $ x = 0.9, 0.99, 1.01, 1.1 $) and evaluate $ f(x) = x + 2 $ at these points to observe the behavior of the function as $ x $ approaches 1.

6:47m

Watch next

Master Finding Limits Numerically and Graphically with a bite sized video explanation from Patrick

Start learning

Struggling with Precalculus?

Find the limit by creating a table of values.lim⁡x→1x2−4x−2\lim_{x\rarr1}\frac{x^2-4}{x-2}limx→1​x−2x2−4​

Watch next

Find the limit by creating a table of values.
$\lim_{x\rarr1}\frac{x^2-4}{x-2}$