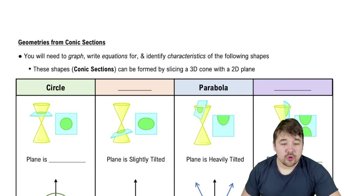
How can you slice a vertically oriented 3D cone to get a 2D parabola?

• A. Slice the cone with a horizontal plane.
• B. Slice the cone with a slightly tilted plane.
• C. Slice the cone with a heavily tilted plane.
• D. Slice the cone with a vertical plane.

Answer: (C)

Verified step by step guidance

1. Understand the geometry of a cone: A cone is a three-dimensional shape with a circular base and a single vertex. When slicing a cone, the orientation of the plane relative to the cone determines the shape of the cross-section.
2. Consider the orientation of the plane: To obtain a parabola, the plane must be tilted relative to the axis of the cone. A horizontal plane will produce a circle, while a vertical plane will produce a hyperbola.
3. Visualize the slicing process: Imagine a plane that is tilted at an angle, not parallel to the base and not perpendicular to the axis of the cone. This plane should intersect the cone in such a way that it cuts through both the curved surface and the base.
4. Determine the angle of tilt: The plane should be heavily tilted, meaning it is angled enough to intersect the cone in a way that the cross-section forms a parabola. This requires the plane to be neither too shallow nor too steep.
5. Recognize the resulting shape: When the plane is heavily tilted, the intersection with the cone will form a parabola. This is because the curve of the cone and the angle of the plane create a parabolic shape in the cross-section.