The mass of the sun is 2.0 x 10^30 kg. A 5.0 x 10^14 kg comet is 75 million kilometers from the sun. What is the magnitude of the comet's acceleration toward the sun?

Key Concepts

Newton's Law of Universal Gravitation

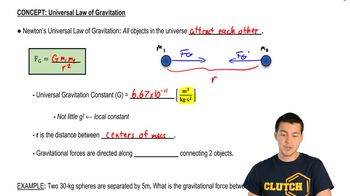
Newton's Law of Universal Gravitation states that every mass attracts every other mass with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centers. This law is fundamental for understanding gravitational interactions, such as the force between the sun and the comet in this scenario.

Gravitational Acceleration

Gravitational acceleration is the acceleration of an object due to the gravitational force exerted by a massive body, such as the sun. It can be calculated using the formula a = F/m, where F is the gravitational force and m is the mass of the object experiencing the force. This concept is crucial for determining how quickly the comet is pulled toward the sun.

Distance in Gravitational Calculations

In gravitational calculations, the distance between the centers of two masses is critical, as it affects the gravitational force and acceleration. In this case, the distance of 75 million kilometers must be converted to meters for accurate calculations, as gravitational equations typically use SI units. Understanding how distance influences gravitational interactions is essential for solving the problem.