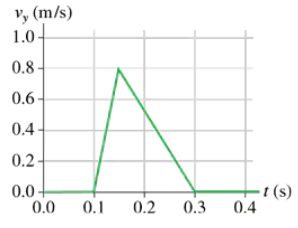
FIGURE EX2.8 is a somewhat idealized graph of the velocity of blood in the ascending aorta during one beat of the heart. Approximately how far, in cm, does the blood move during one beat?

Verified step by step guidance

1. Step 1: Understand the problem. The graph provided shows the velocity of blood in the ascending aorta as a function of time during one beat of the heart. To find the distance the blood moves, we need to calculate the area under the velocity-time graph, as distance is the integral of velocity over time.
2. Step 2: Break the graph into geometric shapes. The graph consists of three distinct regions: a triangle from t = 0 to t = 8 seconds, another triangle from t = 8 to t = 16 seconds, and a rectangle from t = 16 to t = 20 seconds. Each shape's area corresponds to the distance traveled during that time interval.
3. Step 3: Calculate the area of the first triangle (t = 0 to t = 8 seconds). The formula for the area of a triangle is \( \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \). Here, the base is 8 seconds and the height is 20 m/s.
4. Step 4: Calculate the area of the second triangle (t = 8 to t = 16 seconds). Again, use \( \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \). The base is 8 seconds and the height is 20 m/s.
5. Step 5: Calculate the area of the rectangle (t = 16 to t = 20 seconds). The formula for the area of a rectangle is \( \text{Area} = \text{base} \times \text{height} \). Here, the base is 4 seconds and the height is 10 m/s. Add the areas of all three shapes to find the total distance traveled during one beat of the heart.

Key Concepts

Velocity-Time Graph

A velocity-time graph represents an object's velocity over time. The area under the curve of this graph indicates the displacement of the object. In this case, the graph shows the velocity of blood in the aorta during a heartbeat, allowing us to calculate how far the blood travels by finding the area under the curve.

Area Under the Curve

The area under a velocity-time graph can be calculated using geometric shapes, such as rectangles and triangles. This area represents the total displacement of the object over the given time interval. For the blood flow in the aorta, calculating this area will provide the distance the blood moves during one heartbeat.

Units of Measurement

Understanding the units of measurement is crucial for interpreting the graph correctly. In this case, velocity is measured in meters per second (m/s) and time in seconds (s). The resulting displacement will be in meters, which can be converted to centimeters for the final answer, as the question asks for the distance in centimeters.