Heat Engines & PV Diagrams: Videos & Practice Problems

In a cyclic heat engine process, work is calculated using the area enclosed in the PV diagram. For isobaric, isovolumetric, and isothermal processes, specific heat equations are applied: q = ncpΔT for isobaric, q = ncvΔT for isovolumetric, and q=w for isothermal. The total work done is W = q_h-q_c, emphasizing the importance of understanding energy flow in thermodynamics.

Calculating Work in Heat Engines Using PV Diagrams

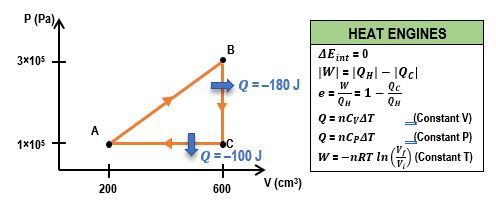
In thermodynamics, understanding the relationship between pressure (P), volume (V), and heat transfer is crucial, especially when analyzing heat engines. A heat engine operates through a cyclic process, which means it returns to its initial state after completing a series of steps. This cycle can be represented on a PV diagram, where the area enclosed by the cycle corresponds to the work done by the engine.

In a typical heat engine cycle, there are distinct processes: isobaric (constant pressure), isovolumetric (constant volume), and isothermal (constant temperature). For example, consider a system with 2 moles of a monoatomic gas undergoing a cyclic process. The steps include:

• Isobaric Process (A to B): Heat is removed from the gas at constant pressure. The heat transfer (q) can be calculated using the formula: q = nC_P \Delta T, where n is the number of moles, C_P is the molar specific heat at constant pressure, and ΔT is the change in temperature. For a monoatomic gas, C_P is given by \(C_P = \frac{5}{2}R\), where R is the ideal gas constant (approximately 8.314 J/(mol·K)). If the temperature changes from 200 K to 100 K, the heat transfer results in a negative value, indicating heat removal.
• Isovolumetric Process (B to C): Heat is added at constant volume. The heat transfer can be calculated using the formula: q = nC_V \Delta T, where C_V is the molar specific heat at constant volume, which for a monoatomic gas is \(C_V = \frac{3}{2}R\). If the temperature changes from 100 K to 200 K, this process results in a positive heat transfer value.
• Isothermal Process (C to A): The gas expands isothermally, meaning the temperature remains constant. In this case, the heat transfer is equal to the work done by the gas, which can be directly provided or calculated based on the system's parameters.

To find the total work done by the heat engine, one can use the relationship between heat transfer and work. The work done by the engine is given by the difference between the heat added from the hot reservoir and the heat removed to the cold reservoir:

W = Q_H - Q_C

Here, Q_H is the total heat added during the cycle, which is the sum of the positive heat transfers, and Q_C is the absolute value of the heat removed. It is important to ensure that the signs are correctly interpreted, as heat removed is considered negative in calculations. The final work done by the engine can be calculated by substituting the values obtained from the heat transfer calculations.

In summary, analyzing a heat engine's performance involves understanding the cyclic processes represented on a PV diagram, calculating heat transfers for each process, and using these values to determine the work done by the engine. This approach not only reinforces the principles of thermodynamics but also highlights the practical applications of these concepts in real-world systems.

Example 1

In analyzing a heat engine represented in a PV diagram, it's essential to understand that heat engines operate in cycles. The work done by the engine over a complete cycle can be calculated using the relationship between the heat transferred from the hot reservoir (\(Q_H\)) and the heat expelled to the cold reservoir (\(Q_C\)). The fundamental equation governing this relationship is:

\(W = Q_H - Q_C\)

Here, \(W\) represents the work done by the engine. In many cases, the work done can also be determined by calculating the area enclosed within the cycle on the PV diagram. For a rectangular area, the work can be computed as:

\(W = \text{Base} \times \text{Height}\)

In this example, the base is the difference in volume (0.15 m³) and the height is the pressure (300 Pa). Thus, the work done is:

\(W = 0.15 \, \text{m}^3 \times 300 \, \text{Pa} = 45 \, \text{J}\)

Next, to find the total heat transfer from the hot reservoir (\(Q_H\)), we can rearrange the work equation to solve for \(Q_H\):

\(Q_H = W + Q_C\)

In this scenario, the heat expelled to the cold reservoir consists of two components, \(Q_C = -90 \, \text{J}\) and \(Q_C = -25 \, \text{J}\). When calculating \(Q_H\), we treat these values as positive contributions to the total heat expelled:

\(Q_C = 90 + 25 = 115 \, \text{J}\)

Substituting the known values into the equation gives:

\(Q_H = 45 \, \text{J} + 115 \, \text{J} = 160 \, \text{J}\)

This result indicates that the total heat transferred from the hot reservoir is 160 joules. The calculations align with the energy flow diagram, confirming that the heat engine effectively converts the difference between the heat absorbed and the heat expelled into work.

 A heat engine follows the cycle shown below. What is the thermal efficiency (%) of this engine?

• A. 58.8%
• B. 99.9%
• C. 14.3%
• D. 12.5%

Answer: (D)

Here’s what students ask on this topic:

What is a PV diagram and how is it used in thermodynamics?

A PV diagram, or pressure-volume diagram, is a graphical representation of the changes in pressure (P) and volume (V) in a thermodynamic system. It is used to visualize the processes that a gas undergoes, such as isobaric (constant pressure), isovolumetric (constant volume), and isothermal (constant temperature) processes. In thermodynamics, PV diagrams are crucial for understanding the work done by or on the system, as the area enclosed by a cycle on the PV diagram represents the net work done during that cycle.

How do you calculate work done by a heat engine using a PV diagram?

To calculate the work done by a heat engine using a PV diagram, you need to find the area enclosed by the cycle on the diagram. For a cyclic process, the work done (W) is the area inside the loop. If the process involves simple geometric shapes, you can use basic geometry to find the area. For more complex shapes, you may need to use calculus. The work done is positive if the cycle runs clockwise and negative if it runs counterclockwise.

What are the key equations for calculating heat transfer in isobaric, isovolumetric, and isothermal processes?

For an isobaric process (constant pressure), the heat transfer (q) is given by: $q=n{c}_p∆T$. For an isovolumetric process (constant volume), the heat transfer is: $q=n{c}_v∆T$. For an isothermal process (constant temperature), the heat transfer is equal to the work done: $q=w$.

What is the relationship between heat added, heat removed, and work done in a heat engine?

In a heat engine, the relationship between the heat added (q_h), heat removed (q_c), and work done (W) is given by the equation: $W=q$_h-q_c. Here, q_h is the heat absorbed from the hot reservoir, and q_c is the heat expelled to the cold reservoir. The work done by the engine is the difference between the heat added to the system and the heat removed from it.

Why do heat engines operate in cyclic processes?

Heat engines operate in cyclic processes to continuously convert heat energy into work. In a cyclic process, the system returns to its initial state at the end of each cycle, allowing the engine to repeat the process indefinitely. This cyclic nature ensures that the engine can continuously absorb heat from a hot reservoir, perform work, and expel waste heat to a cold reservoir, maintaining a steady operation over time.