Work Done Through Multiple Processes: Videos & Practice Problems

In thermodynamics, calculating work done during multiple processes involves summing the work from each individual process. For isobaric processes, work is calculated using the equation $w=p\mathrm{∆v}$, while isovolumetric processes yield zero work due to constant volume. The total work depends on the path taken, illustrating path dependence in thermodynamic systems. Understanding these concepts is crucial for solving complex thermodynamic problems effectively.

Calculating Works For Multiple Thermodynamic Processes

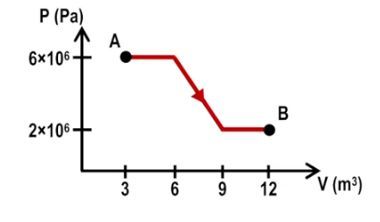
In thermodynamics, calculating the work done during multiple processes is essential for understanding energy transfer within a system. When a system transitions through various states, such as from point A to point B and then from point B to point C, the total work done can be determined by summing the work from each individual process. For instance, if the work done from A to B is 100 joules and from B to C is 80 joules, the total work done is simply the sum: 100 + 80 = 180 joules.

The general formula for total work done over multiple processes is expressed as:

$$W_{\text{total}} = W_1 + W_2 + \ldots + W_n$$

In many scenarios, you will need to calculate the work for each process based on specific thermodynamic conditions. There are four primary types of thermodynamic processes that frequently arise: isobaric, isovolumetric (or isochoric), isothermal, and adiabatic. This summary will focus on isobaric and isovolumetric processes.

An isobaric process occurs at constant pressure. In a PV diagram, this is represented by a horizontal line. The work done during an isobaric process can be calculated using the equation:

$$W = P \Delta V$$

where \(P\) is the constant pressure and \(\Delta V\) is the change in volume.

Conversely, an isovolumetric process maintains constant volume, which means there is no change in volume (\(\Delta V = 0\)). This is depicted as a vertical line on a PV diagram. Since there is no volume change, the work done in an isovolumetric process is:

$$W = 0$$

To illustrate these concepts, consider a system transitioning from point A to point C via two different paths: A to B to C and A to D to C. In the first path, the segment from A to B is isobaric, while from B to C is isovolumetric. The work done from A to B can be calculated using the isobaric formula, while the work from B to C is zero due to the isovolumetric nature. Thus, the total work for this path is simply the work from A to B.

In the second path, A to D is isovolumetric (resulting in zero work), and D to C is isobaric. Here, the total work is solely determined by the work done from D to C. This demonstrates that the work done between two states is path-dependent, meaning it varies based on the specific route taken through the thermodynamic processes.

Understanding these principles is crucial for solving complex thermodynamic problems and analyzing energy changes in various systems.

How much work is done on a gas that expands from A to B along the path shown below?

• A. 9 × 10⁷ J
• B. 3.6 × 10⁷ J
• C. 3.3 × 10⁷ J
• D. 1.2 × 10⁷ J

Answer: (B)

A gas with an initial volume of 0.2 m³ is heated at constant volume, and the pressure increases from 2×10⁵ Pa to 5×10⁵. Then, it compresses at constant pressure until it reaches a final volume of 0.12 m³. Draw the two processes in the PV diagram below and find the total work done by the gas.

• A. - 1.6 × 10⁴ J
• B. 4 × 10⁴ J
• C. 0 J
• D. - 4 × 10⁴ J

Answer: (D)

Here’s what students ask on this topic:

How do you calculate the total work done in multiple thermodynamic processes?

To calculate the total work done in multiple thermodynamic processes, you sum the work done in each individual process. For example, if a system goes from point A to B and then from B to C, the total work is the sum of the work done from A to B and B to C. Mathematically, this is expressed as:

$W_{\mathrm{total}}=W_1+W_2+...$

Each process may involve different types of thermodynamic processes like isobaric (constant pressure) or isovolumetric (constant volume). For isobaric processes, the work is calculated using $W=p\mathrm{∆v}$, while for isovolumetric processes, the work is zero.

What is the work done in an isobaric process?

In an isobaric process, the pressure remains constant while the volume changes. The work done in an isobaric process is calculated using the equation:

$W=p\mathrm{∆v}$

Here, $p$ is the constant pressure and $\mathrm{∆v}$ is the change in volume. For example, if the pressure is 4000 Pa and the volume changes from 2 m³ to 5 m³, the work done is:

$W=4000(5-2)=12000J$

Why is the work done in an isovolumetric process zero?

In an isovolumetric process, the volume remains constant while the pressure changes. Since work is defined as the product of pressure and the change in volume, and the change in volume is zero, the work done is also zero. Mathematically, this is expressed as:

$W=p\mathrm{∆v}$

Here, $\mathrm{∆v}$ is zero, so:

$W=0$

This means no work is done in an isovolumetric process.

What is path dependence in thermodynamics?

Path dependence in thermodynamics refers to the concept that the work done by a system depends on the specific path taken between two states. Even if the initial and final states are the same, different paths can result in different amounts of work done. This is because work is calculated as the area under the curve on a PV diagram, and different paths can enclose different areas. For example, in a multi-step process, the total work done can vary depending on whether the path involves isobaric, isovolumetric, isothermal, or adiabatic processes.

How do you calculate work done in an isothermal process?

In an isothermal process, the temperature remains constant. For an ideal gas, the work done in an isothermal process can be calculated using the equation:

$W=nRTln\left(\frac{V}{f}\right)$

Here, $n$ is the number of moles of gas, $R$ is the universal gas constant, $T$ is the temperature, and $Vf$ and $Vi$ are the final and initial volumes, respectively. This equation accounts for the fact that the temperature remains constant, and the work done is related to the natural logarithm of the volume ratio.