Cyclic Thermodynamic Processes - Online Tutor, Practice Problems & Exam Prep

Cyclic thermodynamic processes involve a system returning to its initial state after a series of steps. The total work done in such a cycle equals the area enclosed within the PV diagram loop, calculated using the equation for work in isobaric processes. Additionally, the change in internal energy over a complete cycle is zero, indicating that the total heat transfer equals the total work done. This highlights the conservation of energy principle in thermodynamics, emphasizing the relationship between heat, work, and internal energy.

Properties of Cyclic Thermodynamic Processes

Hey, guys. So we've solved lots of problems with PV diagrams. But one of the most important and common ones that you'll see is one where you start off at some position in the PV diagram. You'll do a sequence of steps and then you'll end right back where you started. It basically just goes in a loop like this. These are called cyclic thermodynamic processes, and there are a couple of really important properties that you need to know about them. In this video, we're going to dive right in. We're going to solve this problem together, and let's go ahead and check it out.

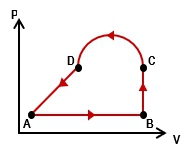
As a cyclic process is one where a system or gas completes a sequence of steps but returns to its initial state. So that's what a cycle is. It returns back to the initial states. There are 2 important properties here. Rather than tell you, I want to show you. So let's just go ahead and take a look at our problem here. So we have this ideal gas and it goes through this process. We want to calculate the work that's done by the gas over the cycle, so the total amount of work done. So how do we do that? Well, let's see.

In part a, if we want to calculate the total amount of work done remember, this is just a bunch of processes sort of strung together. The way we calculate the net work or the total work is you just have to add up all the works done by all these individual processes. Right? We've done that before. So, basically, if I have from a to b and b to c and so on and so forth, the total work will just be the work done across all of these different steps. So the work done from a to b, b to c, c to d, and then the work done from d back to a.

It might seem there are a lot of terms and we're going to have to go calculate a lot of stuff. But let's just go ahead and refer to our table here to make some of these things really easy. So if you think about this sort of square here or rectangle is really made up of 2 different types of steps, isobaric and isovolumetric. What's easy about that is we have the work equations for both of these. It turns out what happens is, remember, in isovolumetric processes, the work done is equal to 0. So that means from a to b, there is no work done because there's no change in volume. Right? And then from c to d, this is also a vertical line, so there's no work done here.

Really, instead of 4 times, we only have 2. These two are isobaric processes, which means we'll be able to use p delta v. So, that just means we're going to take this work equation and it simplifies to the work done from b to c. That's going to be the pressure at b. It's the pressure here. So this is \( p_b \times \Delta v \), from b to c plus the work the pressure done at \( p \), the pressure done here at d. Sorry. That's \( p_d \) here, and then times the change in the volume from d back to a.

So let's take a look at this. Basically, I'm just going to start plugging in some numbers here. \( p_b \) is 35. What's the change in volume from b to c? We're going from 28 to 40 here. So what that means here is that this \( \Delta v \) is equal to 12 from here to here. Alright? So, \( 28 \), you know, the difference between 28 and 40. This is going to be 12. And then what about actually, let us go ahead and plug it in, you know, \( 40 - 28 \) to do final minus initial. So then what about this \( p_d \) here? This is going to be 15, and then the change in the volume here, now from d back to a, remember that this arrow here goes to the left. So my final minus initial is actually \( 28 - 40 \). So it's going to be \( 28 - 40 \).

So, if you go ahead and work this out here, what you're going to end up getting is that the total amount of work done over this entire cycle is 240 joules. Alright? So that's the answer. Let's move on to part b now. In part b, we want to calculate the area enclosed within the loop. The area enclosed is going to be this area that's sort of enclosed insideacji

Signs in a Three-Step Cyclic Process

Hey, guys. So let's take a look at this problem here. This is a kind of conceptual question. There are no numbers involved here. You can sort of do all of this just with logic, but basically what we have is this process that runs a cycle in a PV diagram. So it goes in a loop and it starts back where it ends. We want to complete this table not by calculating a bunch of numbers, but just by inserting signs, whether it's positive, negative, or 0 for each one of these terms here: q, w, and delta E internal. Alright? So let's get started with the first process from a to b. Now this a to b process is an isobaric process. Now if we're trying to relate these variables like heat, work, and internal energy, we're always going to start off with the first law of thermodynamics. Right? So what happens here is that we have delta E internal, the change in internal energy of the system, equals heat added to the system minus the work done by the system. Now we know that this change in internal energy is a positive number. One way you can make sense of this is that if you look sort of like draw out a bunch of isotherms, you're sort of getting farther away from the origin, so the temperature should increase and the internal energy increases, right? That's one way you can make sense of that. What about these other two variables Q and W? Well, remember that for whenever you are moving in a PV diagram to the right, then the area that is underneath the curve here is going to be positive. So the area is positive for underneath the curve anytime you are moving to the right on a PV diagram. That's something that we've said before in a previous video. So therefore, if this is going to be positive, then what about this heat? Well, you can kind of rearrange this equation and figure this out. If you rearrange this, you're going to get the delta E internal of the system, plus the work done by the system, equals the heat added to the system. Right? So this is q 2. So if this is a positive number and this is a positive number, then no matter what the heat on the other side of the equation also has to be a positive number. So basically these are both positives in our table. Alright? So it's kind of just using logic, you know, logical reasoning to figure out those numbers or those signs here. Let's move on to the second piece of this cyclic process. So from B to C. Now from B to C is an isovolumetric process running straight up on the PV diagram here. We're told that the heat transfer is going to be positive. What about the work here? Well, remember that the key characteristic of an isovolumetric process is that there is no work done. It's just 0. So this is going to be 0 over here. Alright. What about the delta E internal? Remember, you're just going to write out your first law of thermodynamics. Delta E internal equals q2 minus w by. Now what we did is we just eliminated this variable here. There is no work done by the gas. So what happens here is that this is a positive number, then the delta E internal also has to be positive. Right? This also has to be positive. One way you can think about this is that, again, these are the isotherms. You're still getting farther away from the origin, so you're increasing in internal energy. So what about c back to a? That's our last process. Now this is not an isobaric or an isovolumetric, so we can't really use any of these equations that we have here. This was in one of our special thermodynamic processes. So let's see. How do we figure this out? Well, so we have delta e internal of equals q2 minus w by. Alright. The problem is that we don't really know what any of these variables are. We're missing one key characteristic about what type of thermodynamic process this is. This is a cycle. So remember that the key characteristic of a cycle here is that delta E for the cycle is equal to 0. So what that means here is that delta e from a to b, plus delta e from b to c, plus Delta E from C to A should equal 0. You should have no change in internal energy. Now what we just found here was that these two processes, the first two, had positive changes in internal energy. So in other words, this is positive and this is also positive. So what happens is in order for the total change in internal energy to be 0 over the entire cycle, then that means that this number here has to be negative, right? If this is 23, this has to be negative 5 so that it all cancels out to 0. It's just making up some numbers here, right? So that's how you figure out this sign here. This has to be negative because of the properties of a cyclic process. What about the work and the heats? Well, again, we're going to use the same rule that we did over here. Whenever you're moving to the left, overall to the left on a PV diagram, the area, so the area that is underneath the graph like this is going to be negative. So this work done by from C back to A is going to equal negative. Right? So that has to be negative. And then finally, what about the q? Well, what happens here is if this is a negative number and this is a negative number, then when you rearrange this, what you're going to get here is the delta e internal of plus w by equals q 2. So if this is negative and this is negative, then q 2 also has to be negative. So all these are negative here on the bottom row. Alright. So that's kind of a conceptual example. You're using a lot of properties of cyclic processes and the first law of thermodynamics to solve for them. So let me know guys if you guys have any questions. That's it for this one.

An ideal gas is taken through the four processes shown below. The changes in internal energy for three of these processes are as follows: ΔE_AB = +82 J; ΔE_BC = +15 J; ΔE_DA = –56 J. Find the change in internal energy for the process from C to D.

• A. - 153 J
• B. 41 J
• C. - 41 J
• D. Cannot determine

Heat Added Over Complete Cycle

Alright, guys. So let's take a look at our example problem. So we have this gas that's undergoing this cyclic thermodynamic process in our PV diagram, and what we want to do is calculate the total amount of heat that's added over a complete cycle. So basically, we just want to figure out, well, what is \(q_{\text{total}}\)? Now there are a couple of ways you might think about this. You might think, well, the total amount of heat is just going to be if I add together the heats from all of the processes. So for example, this is going to be \(q_{\text{A to B}} + q_{\text{B to C}} + q_{\text{C back to A}}\). Now you might be thinking this because, well, let's see, B to C is an isobaric process. That's ISO, and so therefore we have an equation for that. Right? So we could probably figure that out. This is the C to A process is going to be an isovolumetric and we also have an equation for that. The trouble is we don't really have an equation when it comes to this A to B process. This isn't one of our special processes, so we don't have an equation to calculate just the heat for that. Alright? So this actually is not going to work because there's no way to figure out what \(q_{\text{AB}}\) is. So this actually isn't going to work, and instead, we're going to have to think about another property of cyclic processes that's going to help us. So remember that for a cyclic process, the change in the internal energy is always equal to zero. If you start and end in the same place on a PV diagram, there's no change in internal energy. So remember what that means is that the \(q\) over the cycle is equal to \(w\) over the cycle, right, by the first law of thermodynamics. So really this \(q\) over the cycle here is actually just going to be equal to the total amount of work that's done in this cyclic process here. And remember that is actually pretty easy to calculate because the work done over the cycle is actually just the area that is inside of the loop that the sort of cycle runs around. Right? So really this is equal to the work done over the cycle, and it's also equal to the heat that's added over the cycle. Those mean the same exact thing. So really, this is just going to be the area that's inside of the loop, and we have a couple of different ways we can figure this out. Right? Since we have all the values for pressure and volume, we can kind of just use the area of a triangle like this. Right? It's just a triangle, so we can use the area which is \(\frac{1}{2} \times \text{base} \times \text{height}\). So let's just say that this is the height. Let's just say that this is the base like this. So really what happens is that \(q\) for the cycle is going to equal \(\frac{1}{2}\). Now the base here goes from 4 back to 1. So the base here is 3, and then the height of this thing is going to be the difference between 40 and 10. So this base here is 3 and the height here is 30. So I'm just going to do \(\frac{1}{2} \times 3 \times 30\), and what I'm going to get here is 45 joules. Alright? Now we're missing one thing here. We're missing the rules for whether the work is positive or negative. Remember that this work cycle here, if it's clockwise, the work done over the cycle is going to be positive. If it's counterclockwise, the work done by the cycle is going to be negative. What do we have here? We have a loop that's running counterclockwise. It's this one here. So therefore our answer has to have a negative sign. It's going to be negative 45 joules for the work and also the heat added over the cycle. So basically what this means here is that more heat is removed from this cycle here than it is added over. And so the overall heat is going to be negative 45. Alright? So that's it for this one. Let me know if you have any questions.

Here’s what students ask on this topic:

What is a cyclic thermodynamic process?

A cyclic thermodynamic process is one in which a system, such as an ideal gas, undergoes a series of steps and returns to its initial state. This means that the state variables (pressure, volume, and temperature) are the same at the beginning and end of the cycle. In a PV diagram, this process forms a closed loop. The total work done in the cycle is equal to the area enclosed by this loop. Additionally, the change in internal energy over a complete cycle is zero, indicating that the total heat transfer equals the total work done.

How do you calculate the work done in a cyclic process?

The work done in a cyclic process can be calculated by finding the area enclosed by the loop in a PV diagram. For isobaric processes, the work done is given by the equation:

$W=P∆V$

where $P$ is the pressure and $∆V$ is the change in volume. The total work done is the sum of the work done in each individual process within the cycle. For a rectangular loop, the area (and thus the work done) is simply the product of the base and height of the rectangle.

Why is the change in internal energy zero in a cyclic process?

The change in internal energy ($\mathrm{∆E}$) over a complete cycle is zero because internal energy is a state function. This means it depends only on the state of the system, not on the path taken to reach that state. Since the system returns to its initial state in a cyclic process, the initial and final internal energies are the same, resulting in $\mathrm{∆E}=0$. Consequently, the total heat transfer (Q) equals the total work done (W) over the cycle, as given by the first law of thermodynamics: $\mathrm{∆E}=Q-W$.

What is the significance of the direction of the loop in a cyclic process?

The direction of the loop in a cyclic process indicates the sign of the work done. If the loop runs clockwise in a PV diagram, the work done by the system is positive. Conversely, if the loop runs counterclockwise, the work done by the system is negative. This is because the area under the curve represents the work done, and the direction determines whether the work is done on or by the system. Understanding this helps in analyzing energy transfer and efficiency in thermodynamic cycles.

How is the total heat transfer related to the work done in a cyclic process?

In a cyclic process, the total heat transfer (Q) is equal to the total work done (W) by the system. This relationship arises from the fact that the change in internal energy ($\mathrm{∆E}$) over a complete cycle is zero. According to the first law of thermodynamics:

$\mathrm{∆E}=Q-W$

Since $\mathrm{∆E}=0$ for a cyclic process, it follows that $Q=W$. This highlights the conservation of energy principle, emphasizing that the energy added as heat is entirely converted to work over the cycle.