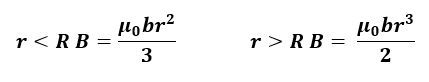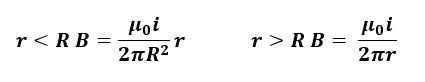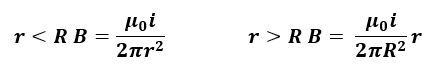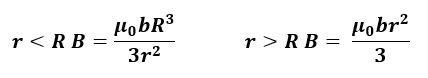Hey, guys. In this video, we're going to be talking about Ampere's law and how to use it. Alright? Let's get to it. Any magnetic field, b, must satisfy the following equation. This is what's known as a line integral. Okay? I am integrating b along some line that creates an arbitrary shape, which I called s. Okay? And this line integral always equals μ₀ Ienclosed. Okay? Notice that this integral has this little circle in the integral sign. All that means is that it's a closed line. Okay? We saw this before for Gauss's law, where we use the circle for the surface integral. Okay? And we said that that was a closed surface. So this has to be a closed loop or a closed line, which we call an amperean loop. Okay? And what Ampere's law says is that this integral depends only on the current enclosed by that amperean loop. And a consequence of that is that the magnetic field is only going to depend upon the current enclosed by that amperean loop as well, just like we saw in Gauss's law. Okay? How to apply this is pretty straightforward. If we take this arbitrary curve s in the figure above me, which surrounds a current I, everywhere along this loop, I can measure the magnetic field, and I can do the dot product with dl. All dl is is it's a very small it's an infinitesimal segment that goes along the curve. Right? So at this point, dl is going to be like this. This point, dl is going to be like this. It just points tangential to the curve. Right? Tangential everywhere. And the magnetic field is going to depend it's going to point in something like this. It would look something like this. It would look something like this. Something like this. Something like this, etcetera. And I could do the dot products, add all those up, integrate it along the curve s, and that would equate to a measurement times the charge enclosed. Okay? Let's apply Ampere's law for a scenario that we've already seen a bunch of times. Using Ampere's law, find the magnetic field due to an infinitely long current carrying wire. So I'm just going to draw the current as going into the page. Okay. Exactly like the figure above. Now, what does that magnetic field look like? Alright. Well, I'm going to stick my thumb in the direction of that current into the page, and the magnetic field is going to curl around it exactly like that. Okay? Which means if I were to draw an empyrean loop that was a circle of some radius r, the magnetic field is always going to be parallel to that line segment dl. Remember, that line segment always points tangential to the curve. Right? So Ampere's law says that this integral, b⋅dl, is going to just be bdl. That dot product is always going to be 1 because they always point parallel. And this equals μ₀ Ienclosed. Okay? Now just like we did for Gauss's law, we cheated a little bit because we knew what the magnetic field looked like. We had to cheat with Gauss's law as well by knowing what the electric field looks like. Furthermore, along this circle, because it's of a constant radius, the magnetic field is constant. So as I go along this circle, as I change my dl, the magnetic field doesn't change. So I can pull that field out. Okay? And lastly, I just need to solve this integral. Well, if I go around the circle one revolution, I've covered a distance equal to the circumference. So that magnetic field is just 2 pi r, and I enclosed is just I. I over 2 pi r. Exactly what we would expect it to be, and what we've seen it to be over and over again. Okay? So Ampere's law tells us what the magnetic field due to an infinitely long wire is much, much more quickly than Biot Savart law does, for instance. Alright. Thanks for watching, guys.
- 0. Math Review31m
- 1. Intro to Physics Units1h 23m
- 2. 1D Motion / Kinematics3h 56m
- Vectors, Scalars, & Displacement13m
- Average Velocity32m
- Intro to Acceleration7m
- Position-Time Graphs & Velocity26m
- Conceptual Problems with Position-Time Graphs22m
- Velocity-Time Graphs & Acceleration5m
- Calculating Displacement from Velocity-Time Graphs15m
- Conceptual Problems with Velocity-Time Graphs10m
- Calculating Change in Velocity from Acceleration-Time Graphs10m
- Graphing Position, Velocity, and Acceleration Graphs11m
- Kinematics Equations37m
- Vertical Motion and Free Fall19m
- Catch/Overtake Problems23m
- 3. Vectors2h 43m
- Review of Vectors vs. Scalars1m
- Introduction to Vectors7m
- Adding Vectors Graphically22m
- Vector Composition & Decomposition11m
- Adding Vectors by Components13m
- Trig Review24m
- Unit Vectors15m
- Introduction to Dot Product (Scalar Product)12m
- Calculating Dot Product Using Components12m
- Intro to Cross Product (Vector Product)23m
- Calculating Cross Product Using Components17m
- 4. 2D Kinematics1h 42m
- 5. Projectile Motion3h 6m
- 6. Intro to Forces (Dynamics)3h 22m
- 7. Friction, Inclines, Systems2h 44m
- 8. Centripetal Forces & Gravitation7h 26m
- Uniform Circular Motion7m
- Period and Frequency in Uniform Circular Motion20m
- Centripetal Forces15m
- Vertical Centripetal Forces10m
- Flat Curves9m
- Banked Curves10m
- Newton's Law of Gravity30m
- Gravitational Forces in 2D25m
- Acceleration Due to Gravity13m
- Satellite Motion: Intro5m
- Satellite Motion: Speed & Period35m
- Geosynchronous Orbits15m
- Overview of Kepler's Laws5m
- Kepler's First Law11m
- Kepler's Third Law16m
- Kepler's Third Law for Elliptical Orbits15m
- Gravitational Potential Energy21m
- Gravitational Potential Energy for Systems of Masses17m
- Escape Velocity21m
- Energy of Circular Orbits23m
- Energy of Elliptical Orbits36m
- Black Holes16m
- Gravitational Force Inside the Earth13m
- Mass Distribution with Calculus45m
- 9. Work & Energy1h 59m
- 10. Conservation of Energy2h 54m
- Intro to Energy Types3m
- Gravitational Potential Energy10m
- Intro to Conservation of Energy32m
- Energy with Non-Conservative Forces20m
- Springs & Elastic Potential Energy19m
- Solving Projectile Motion Using Energy13m
- Motion Along Curved Paths4m
- Rollercoaster Problems13m
- Pendulum Problems13m
- Energy in Connected Objects (Systems)24m
- Force & Potential Energy18m
- 11. Momentum & Impulse3h 40m
- Intro to Momentum11m
- Intro to Impulse14m
- Impulse with Variable Forces12m
- Intro to Conservation of Momentum17m
- Push-Away Problems19m
- Types of Collisions4m
- Completely Inelastic Collisions28m
- Adding Mass to a Moving System8m
- Collisions & Motion (Momentum & Energy)26m
- Ballistic Pendulum14m
- Collisions with Springs13m
- Elastic Collisions24m
- How to Identify the Type of Collision9m
- Intro to Center of Mass15m
- 12. Rotational Kinematics2h 59m
- 13. Rotational Inertia & Energy7h 4m
- More Conservation of Energy Problems54m
- Conservation of Energy in Rolling Motion45m
- Parallel Axis Theorem13m
- Intro to Moment of Inertia28m
- Moment of Inertia via Integration18m
- Moment of Inertia of Systems23m
- Moment of Inertia & Mass Distribution10m
- Intro to Rotational Kinetic Energy16m
- Energy of Rolling Motion18m
- Types of Motion & Energy24m
- Conservation of Energy with Rotation35m
- Torque with Kinematic Equations56m
- Rotational Dynamics with Two Motions50m
- Rotational Dynamics of Rolling Motion27m
- 14. Torque & Rotational Dynamics2h 5m
- 15. Rotational Equilibrium3h 39m
- 16. Angular Momentum3h 6m
- Opening/Closing Arms on Rotating Stool18m
- Conservation of Angular Momentum46m
- Angular Momentum & Newton's Second Law10m
- Intro to Angular Collisions15m
- Jumping Into/Out of Moving Disc23m
- Spinning on String of Variable Length20m
- Angular Collisions with Linear Motion8m
- Intro to Angular Momentum15m
- Angular Momentum of a Point Mass21m
- Angular Momentum of Objects in Linear Motion7m
- 17. Periodic Motion2h 9m
- 18. Waves & Sound3h 40m
- Intro to Waves11m
- Velocity of Transverse Waves21m
- Velocity of Longitudinal Waves11m
- Wave Functions31m
- Phase Constant14m
- Average Power of Waves on Strings10m
- Wave Intensity19m
- Sound Intensity13m
- Wave Interference8m
- Superposition of Wave Functions3m
- Standing Waves30m
- Standing Wave Functions14m
- Standing Sound Waves12m
- Beats8m
- The Doppler Effect7m
- 19. Fluid Mechanics2h 27m
- 20. Heat and Temperature3h 7m
- Temperature16m
- Linear Thermal Expansion14m
- Volume Thermal Expansion14m
- Moles and Avogadro's Number14m
- Specific Heat & Temperature Changes12m
- Latent Heat & Phase Changes16m
- Intro to Calorimetry21m
- Calorimetry with Temperature and Phase Changes15m
- Advanced Calorimetry: Equilibrium Temperature with Phase Changes9m
- Phase Diagrams, Triple Points and Critical Points6m
- Heat Transfer44m
- 21. Kinetic Theory of Ideal Gases1h 50m
- 22. The First Law of Thermodynamics1h 26m
- 23. The Second Law of Thermodynamics3h 11m
- 24. Electric Force & Field; Gauss' Law3h 42m
- 25. Electric Potential1h 51m
- 26. Capacitors & Dielectrics2h 2m
- 27. Resistors & DC Circuits3h 8m
- 28. Magnetic Fields and Forces2h 23m
- 29. Sources of Magnetic Field2h 30m
- Magnetic Field Produced by Moving Charges10m
- Magnetic Field Produced by Straight Currents27m
- Magnetic Force Between Parallel Currents12m
- Magnetic Force Between Two Moving Charges9m
- Magnetic Field Produced by Loops and Solenoids42m
- Toroidal Solenoids aka Toroids12m
- Biot-Savart Law (Calculus)18m
- Ampere's Law (Calculus)17m
- 30. Induction and Inductance3h 37m
- 31. Alternating Current2h 37m
- Alternating Voltages and Currents18m
- RMS Current and Voltage9m
- Phasors20m
- Resistors in AC Circuits9m
- Phasors for Resistors7m
- Capacitors in AC Circuits16m
- Phasors for Capacitors8m
- Inductors in AC Circuits13m
- Phasors for Inductors7m
- Impedance in AC Circuits18m
- Series LRC Circuits11m
- Resonance in Series LRC Circuits10m
- Power in AC Circuits5m
- 32. Electromagnetic Waves2h 14m
- 33. Geometric Optics2h 57m
- 34. Wave Optics1h 15m
- 35. Special Relativity2h 10m
Ampere's Law (Calculus): Study with Video Lessons, Practice Problems & Examples
 Created using AI
Created using AIAmpere's law relates the magnetic field (B) around a closed loop to the current (I) enclosed by that loop, expressed as a line integral: ∫ ○ sBdl = μ0Ienclosed. For an infinitely long wire, the magnetic field curls around the wire, allowing for straightforward calculations of B using Ampere's law, yielding B = μ0I / (2πr). This method simplifies finding magnetic fields compared to Biot-Savart law.
Ampere's Law with Calculus
Video transcript
Magnetic Field Inside a Solenoid
Video transcript
Hey guys, let's do an example. What is the magnetic field along the axis of a solenoid? Okay, so let's take some sort of solenoid like this. It's got some current going through it. It's got n number of loops spread out over a distance, l. Now, what is the magnetic field going to look like straight down the center of this solenoid? We want to use Ampere's law to find what that magnetic field is. Ampere's law tells us that the line integral b·dl across an Amperean loop has to equal μ_0 times the charge enclosed. Now, the particular Amperian loop I'm going to choose looks like this. I'm going to go down the axis of the solenoid, only for the length of the solenoid, where I know that the magnetic field is constant and straight. Like for Gauss's law, we are going to cheat a bit because we already know things about what the magnetic field should be before using Ampere's law. Then I'm going to go straight up. So it's a 90 degree angle straight up. Up. Infinitely high. So there is a gap here. And then I'm going to come back across. This little gap here takes us all the way up to infinity. So, this Amperian loop has four steps. It has step 1, which is along the axis, step 2, which is straight up perpendicular to the axis all the way up to infinity, step 3, which is parallel to the axis coming back but infinitely far away. And step 4, which is perpendicular to the axis coming back down. So this integral becomes the first path, b·dl, plus the second path, b·dl, plus the third path, b·dl, plus the fourth path, b·dl. Now the thing about paths 2 and paths 4 is that above the solenoid, the magnetic field line points parallel to the axis. So you're going to get a magnetic field line that is perpendicular to dl. Here's dl. Well, that magnetic field line actually points in the opposite direction. Because they are perpendicular, the dot product is always 0. So right away, for 2 and for 4, it's 0. Now what about 3? The thing is, 3 is parallel to the axis, so there would be a component of the magnetic field along it. The problem is that it's infinitely far away. Things in physics always drop to 0 when you go infinitely far away. Otherwise, two objects that are infinitely far apart could still interact with one another. Gravity goes to 0, gravitational potential energy goes to 0, electric force, electric potential energy, electric potential, electric field, etcetera, they all become 0 infinitely far away so that two things can't interact when they are infinitely far away. So the magnetic field line along path 3 is 0. This only leaves path 1. And they're parallel along path 1. So this integral becomes bdl from 0 to l, just the length of that axis, which runs the length of the solenoid, capital L. The magnetic field is going to be constant along the axis, so I can pull it out. And this just becomes bL. Now, this is the left half of Ampere's law. What about the right half of Ampere's law? That tells us it's μ_0 times the enclosed current. If there was a single loop here, just a single loop, we would have a single current I. For each loop, we have an additional current I. How many loops are there? There are n loops. So this is times n. Each of them carries I. So if we get out of the way, so we see the equation right here, this whole thing becomes bL equals μ_0nI or b is μ_0n over lI. This is the exact equation for a solenoid that we're expecting. Sometimes written like this, where little n is the number of turns per unit length. Okay guys? Thanks for watching.
A solid, cylindrical conductor carries a uniform current density, J. If the radius of the cylindrical conductor is R, what is the magnetic field at a distance ? from the center of the conductor when r < R? What about when r > R?
Do you want more practice?
More setsHere’s what students ask on this topic:
What is Ampere's Law and how is it used to calculate the magnetic field?
Ampere's Law states that the line integral of the magnetic field around a closed loop is equal to the permeability of free space times the current enclosed by the loop. Mathematically, it is expressed as:
To use Ampere's Law, choose an Amperian loop that simplifies the calculation, often exploiting symmetry. For example, for an infinitely long current-carrying wire, the magnetic field curls around the wire, and the integral simplifies to:
Solving for gives:
 Created using AI
Created using AIHow does Ampere's Law compare to the Biot-Savart Law?
Ampere's Law and the Biot-Savart Law both describe the magnetic field generated by a current, but they are used in different contexts. Ampere's Law is particularly useful for calculating the magnetic field in situations with high symmetry, such as around an infinitely long straight wire or inside a solenoid. It simplifies the calculation by relating the magnetic field to the enclosed current through a line integral:
The Biot-Savart Law, on the other hand, is more general and can be used to calculate the magnetic field at any point in space due to a current element. It is expressed as:
While the Biot-Savart Law is more versatile, Ampere's Law provides a quicker solution in symmetric cases.
 Created using AI
Created using AIWhat is an Amperian loop and how is it chosen?
An Amperian loop is a closed path used in Ampere's Law to calculate the magnetic field around a current-carrying conductor. The choice of the Amperian loop is crucial for simplifying the calculations. Typically, the loop is chosen to exploit the symmetry of the problem. For example, for an infinitely long straight wire, a circular loop centered on the wire is chosen because the magnetic field is tangential and constant in magnitude along the loop. This simplifies the line integral:
For a solenoid, a rectangular loop is often chosen to align with the magnetic field inside and outside the solenoid, simplifying the integral. The goal is to make the integral easy to evaluate by aligning the loop with the symmetry of the magnetic field.
 Created using AI
Created using AIHow do you apply Ampere's Law to find the magnetic field inside a solenoid?
To find the magnetic field inside a solenoid using Ampere's Law, consider a rectangular Amperian loop that runs parallel to the axis of the solenoid. The loop should have one side inside the solenoid and one side outside where the magnetic field is negligible. Inside the solenoid, the magnetic field is uniform and parallel to the axis. The line integral simplifies to:
where is the length of the loop inside the solenoid. According to Ampere's Law:
where is the number of turns per unit length and is the current. Simplifying, we get:
This shows that the magnetic field inside a solenoid is directly proportional to the current and the number of turns per unit length.
 Created using AI
Created using AIWhat is the significance of the closed loop in Ampere's Law?
The closed loop in Ampere's Law, often referred to as an Amperian loop, is significant because it ensures that the line integral of the magnetic field around the loop is equal to the permeability of free space times the total current enclosed by the loop. This closed loop is essential for the application of Ampere's Law:
The closed loop ensures that all contributions to the magnetic field from the enclosed current are accounted for. It also allows for the use of symmetry to simplify calculations, making it easier to determine the magnetic field in various configurations, such as around a straight wire or inside a solenoid.
 Created using AI
Created using AIYour Physics tutor
- A solid conductor with radius a is supported by insulating disks on the axis of a conducting tube with inner r...
- As a new electrical technician, you are designing a large solenoid to produce a uniform 0.150-T magnetic field...
- A closed curve encircles several conductors. The line integral ∲B .dl around this curve is 3.83 * 10^-4 T m. (...
- The value of the line integral of →B ⋅ ds around the closed path in FIGURE EX29.21 is 1.38 x 10⁻⁵ T m. What ar...
- (I) A 2.5-mm-diameter copper wire carries a 28-A dc current (uniform across its cross section). Determine the ...
- You want to get an idea of the magnitude of magnetic fields produced by overhead power lines. You estimate tha...
- (III) Suppose the current in the coaxial cable of Problem 34, Fig. 28–45, is not uniformly distributed, but in...
- (II) A circular conducting ring of radius 𝑅 is connected to two exterior straight wires at two ends of a diam...
- Three long parallel wires are 3.5 cm from one another. (Looking along them, they are at three corners of an eq...
- (III) A coaxial cable consists of a solid inner conductor of radius 𝑅₁ , surrounded by a concentric cylindric...