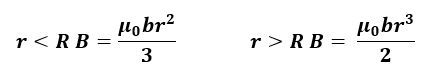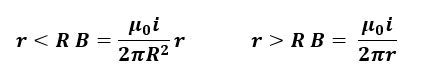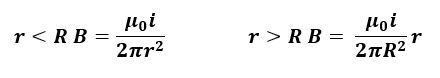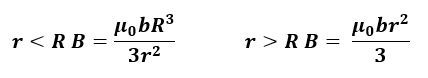Ampere's Law (Calculus): Videos & Practice Problems

Ampere's law relates the magnetic field (B) around a closed loop to the current (I) enclosed by that loop, expressed as a line integral: ∫ ○ sB⁢dl = μ₀I_enclosed. For an infinitely long wire, the magnetic field curls around the wire, allowing for straightforward calculations of B using Ampere's law, yielding B = μ₀I / (2πr). This method simplifies finding magnetic fields compared to Biot-Savart law.

Ampere's Law with Calculus

Ampere's law is a fundamental principle in electromagnetism that relates the magnetic field around a closed loop to the electric current passing through that loop. The law is expressed mathematically as a line integral of the magnetic field, denoted as \( \oint \mathbf{B} \cdot d\mathbf{l} = \mu_0 I_{\text{enc}} \), where \( \mathbf{B} \) is the magnetic field, \( d\mathbf{l} \) is an infinitesimal segment of the loop, \( \mu_0 \) is the permeability of free space, and \( I_{\text{enc}} \) is the current enclosed by the loop. The integral is taken over a closed path, known as an Amperian loop, which is crucial for applying this law.

To apply Ampere's law, consider a scenario with an infinitely long current-carrying wire. If the current \( I \) flows into the page, the magnetic field \( \mathbf{B} \) will circulate around the wire. By using the right-hand rule, you can determine the direction of the magnetic field: if you point your thumb in the direction of the current, your fingers will curl in the direction of the magnetic field lines.

When you choose a circular Amperian loop of radius \( r \) around the wire, the magnetic field is constant in magnitude and direction along the loop. Thus, the line integral simplifies to \( \oint \mathbf{B} \cdot d\mathbf{l} = B \oint d\mathbf{l} = B(2\pi r) \). Setting this equal to \( \mu_0 I \) gives the equation:

\[ B(2\pi r) = \mu_0 I \]

From this, you can solve for the magnetic field \( B \):

\[ B = \frac{\mu_0 I}{2\pi r} \]

This result shows that the magnetic field around an infinitely long wire decreases inversely with distance from the wire, which is a key takeaway from Ampere's law. This method is often more efficient than using the Biot-Savart law for calculating magnetic fields in such scenarios.

Magnetic Field Inside a Solenoid

To determine the magnetic field along the axis of a solenoid, we can apply Ampere's law, which states that the line integral of the magnetic field \( \mathbf{B} \) around a closed loop is equal to the permeability of free space \( \mu_0 \) multiplied by the total current \( I \) enclosed by that loop. The equation can be expressed as:

\[ \oint \mathbf{B} \cdot d\mathbf{l} = \mu_0 I_{\text{enc}} \]

Consider a solenoid with \( n \) turns per unit length and carrying a current \( I \). The solenoid has a length \( L \) and the magnetic field is uniform and directed along its axis. To analyze the magnetic field, we can choose an Amperian loop that runs along the axis of the solenoid for a length \( L \), extends vertically upwards to infinity, runs parallel to the axis at infinity, and then returns downwards to the starting point.

In this configuration, the integral can be broken down into four segments:

1. Along the axis of the solenoid (where the magnetic field is constant).
2. Perpendicular to the axis, extending upwards (where the magnetic field is zero).
3. Parallel to the axis at infinity (where the magnetic field is also zero).
4. Perpendicular to the axis, returning downwards (where the magnetic field is zero).

Only the first segment contributes to the integral, as the magnetic field is zero in the other segments. Thus, we have:

\[ \oint \mathbf{B} \cdot d\mathbf{l} = B \cdot L \]

On the right side of Ampere's law, we need to calculate the enclosed current. Since there are \( n \) loops in the solenoid, the total current enclosed is \( nI \). Therefore, we can express the right side as:

\[ I_{\text{enc}} = nI \]

Substituting this into Ampere's law gives us:

\[ B \cdot L = \mu_0 n I \]

From this, we can solve for the magnetic field \( B \) along the axis of the solenoid:

\[ B = \frac{\mu_0 n I}{L} \]

This equation indicates that the magnetic field inside a long solenoid is directly proportional to the number of turns per unit length \( n \) and the current \( I \) flowing through it, while inversely proportional to the length \( L \) of the solenoid. This relationship is fundamental in understanding the behavior of magnetic fields in solenoids and is crucial for applications in electromagnetism.

A solid, cylindrical conductor carries a uniform current density, J. If the radius of the cylindrical conductor is R, what is the magnetic field at a distance ? from the center of the conductor when r < R? What about when r > R?

• A.
• B.
• C.
• D.

Answer: (B)

Here’s what students ask on this topic:

What is Ampere's Law and how is it used to calculate the magnetic field?

Ampere's Law states that the line integral of the magnetic field $B$ around a closed loop is equal to the permeability of free space $\mu$₀ times the current enclosed by the loop. Mathematically, it is expressed as:

$\oint$_sB⋅dl=μ₀I_enclosed

To use Ampere's Law, choose an Amperian loop that simplifies the calculation, often exploiting symmetry. For example, for an infinitely long current-carrying wire, the magnetic field $B$ curls around the wire, and the integral simplifies to:

$B\cdot 2\pi r=\mu$₀I

Solving for $B$ gives:

$B=\frac{\mu }{}$₀I/2πr

How does Ampere's Law compare to the Biot-Savart Law?

Ampere's Law and the Biot-Savart Law both describe the magnetic field generated by a current, but they are used in different contexts. Ampere's Law is particularly useful for calculating the magnetic field in situations with high symmetry, such as around an infinitely long straight wire or inside a solenoid. It simplifies the calculation by relating the magnetic field to the enclosed current through a line integral:

$\oint$_sB⋅dl=μ₀I_enclosed

The Biot-Savart Law, on the other hand, is more general and can be used to calculate the magnetic field at any point in space due to a current element. It is expressed as:

$dB=\frac{\mu }{}$₀Idl⋅sinθ/4πr²

While the Biot-Savart Law is more versatile, Ampere's Law provides a quicker solution in symmetric cases.

What is an Amperian loop and how is it chosen?

An Amperian loop is a closed path used in Ampere's Law to calculate the magnetic field around a current-carrying conductor. The choice of the Amperian loop is crucial for simplifying the calculations. Typically, the loop is chosen to exploit the symmetry of the problem. For example, for an infinitely long straight wire, a circular loop centered on the wire is chosen because the magnetic field is tangential and constant in magnitude along the loop. This simplifies the line integral:

$\oint$_sB⋅dl=B⋅2πr

For a solenoid, a rectangular loop is often chosen to align with the magnetic field inside and outside the solenoid, simplifying the integral. The goal is to make the integral easy to evaluate by aligning the loop with the symmetry of the magnetic field.

How do you apply Ampere's Law to find the magnetic field inside a solenoid?

To find the magnetic field inside a solenoid using Ampere's Law, consider a rectangular Amperian loop that runs parallel to the axis of the solenoid. The loop should have one side inside the solenoid and one side outside where the magnetic field is negligible. Inside the solenoid, the magnetic field $B$ is uniform and parallel to the axis. The line integral simplifies to:

$\oint$_sB⋅dl=B⋅l

where $l$ is the length of the loop inside the solenoid. According to Ampere's Law:

$B\cdot l=\mu$₀nIl

where $n$ is the number of turns per unit length and $I$ is the current. Simplifying, we get:

$B=\mu$₀nI

This shows that the magnetic field inside a solenoid is directly proportional to the current and the number of turns per unit length.

What is the significance of the closed loop in Ampere's Law?

The closed loop in Ampere's Law, often referred to as an Amperian loop, is significant because it ensures that the line integral of the magnetic field $B$ around the loop is equal to the permeability of free space $\mu$₀ times the total current enclosed by the loop. This closed loop is essential for the application of Ampere's Law:

$\oint$_sB⋅dl=μ₀I_enclosed

The closed loop ensures that all contributions to the magnetic field from the enclosed current are accounted for. It also allows for the use of symmetry to simplify calculations, making it easier to determine the magnetic field in various configurations, such as around a straight wire or inside a solenoid.