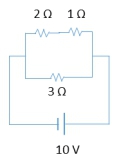
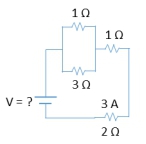
In solving complex circuit problems, it's essential to understand how resistors behave in series and parallel configurations. When resistors are connected in series, the total or equivalent resistance can be calculated by simply adding their resistances together. The formula for equivalent resistance in series is:
R_{eq} = R_1 + R_2 + R_3 + ... + R_n
Conversely, for resistors in parallel, the equivalent resistance is found using the reciprocal formula:
\(\frac{1}{R_{eq}\)} = \(\frac{1}{R_1}\) + \(\frac{1}{R_2}\) + \(\frac{1}{R_3}\) + ... + \(\frac{1}{R_n}\)
In series circuits, the current remains constant across all resistors. For example, if a series circuit has a current of 2 amps, each resistor in that series will also carry 2 amps. This is crucial when determining the current through an equivalent resistor formed by combining series resistors.
In parallel circuits, the voltage across each resistor is the same. If three 9-ohm resistors are connected in parallel and the voltage across them is 5 volts, then each resistor experiences 5 volts. The equivalent resistance for these resistors can be quickly calculated using the shortcut for three identical resistors:
R_{eq} = \(\frac{R}{n}\) = \(\frac{9 \, \text{ohms}\)}{3} = 3 \, \(\text{ohms}\)
To solve circuit problems systematically, follow these three steps:
- Reduce the circuit to a single equivalent resistor using series and parallel combinations.
- Apply Ohm's Law, V = IR, to find the voltage and current for the equivalent resistor.
- Work backwards to determine the voltage and current for each individual resistor based on the relationships established in the first two steps.
For instance, if you have a circuit with a 10-volt battery and a combination of resistors, first find the equivalent resistance. Then, using Ohm's Law, calculate the current drawn from the battery. This current will flow through all series resistors, allowing you to find their individual voltages using the same law.
When working backwards, remember that resistors in series share the same current, while resistors in parallel share the same voltage. This understanding allows you to calculate the unknown values for each resistor effectively.
Finally, ensure that your calculations adhere to Kirchhoff's Current Law, which states that the total current entering a junction must equal the total current leaving it. This principle can help verify your results and ensure consistency throughout your calculations.
By maintaining an organized approach and systematically applying these principles, you can effectively tackle complex circuit problems and gain a deeper understanding of electrical circuits.