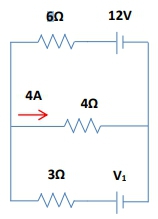
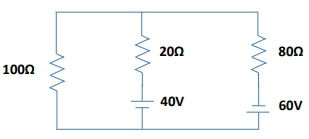
Kirchhoff's Loop Rule: Videos & Practice Problems

Kirchhoff's loop rule states that the sum of all voltages in a closed loop of a circuit equals zero. This principle is crucial for analyzing circuits with multiple voltage sources. When writing loop equations, voltages are added or subtracted based on the direction of current and the loop. For series voltage sources, voltages add if aligned in the same direction and subtract if opposing. To verify calculations, ensure all branches have consistent voltage magnitudes and polarities, applying Ohm's law (V = I × R) for resistors to find voltage drops.

Intro to Kirchhoff's Loop Rule

Kirchhoff's loop rule, also known as Kirchhoff's voltage law, is a fundamental principle in circuit analysis that states the sum of all voltages around a closed loop in a circuit must equal zero. This concept is crucial when dealing with complex circuits that contain multiple voltage sources, as it allows for systematic problem-solving. The essence of the loop rule is straightforward: as you traverse a loop, you will either add or subtract the voltages of the components based on their orientation relative to the direction of the current flow.

To apply Kirchhoff's loop rule effectively, one must first identify the direction of the current and the loop. The voltage across a resistor can be calculated using Ohm's law, expressed as \( V = I \cdot R \), where \( I \) is the current and \( R \) is the resistance. When writing a loop equation, it is essential to assign positive and negative signs to the voltages based on the direction of the current and the loop. If you cross a component from negative to positive, you add that voltage; conversely, if you cross from positive to negative, you subtract it.

For example, consider a loop with two resistors and two batteries. If you start at a point in the loop and move in the direction of the current, you would first encounter a resistor. The voltage across this resistor would be subtracted from the total because you are moving from positive to negative. If you then encounter a battery, the voltage would be added if you cross from negative to positive. This process continues until you return to the starting point, at which point the sum of all voltages should equal zero.

It is important to note that the direction in which you traverse the loop (clockwise or counterclockwise) does not affect the final equation; you will arrive at the same result regardless of the chosen direction. This flexibility allows for greater ease in circuit analysis, as you can select the direction that seems most intuitive for the problem at hand.

In summary, Kirchhoff's loop rule is a powerful tool for analyzing electrical circuits. By carefully considering the direction of current flow and the orientation of circuit elements, you can systematically write loop equations that facilitate the solution of complex circuit problems. Mastery of this rule will significantly enhance your ability to tackle a variety of circuit configurations.

Direction of Current in Loop Equations

In analyzing complex electrical circuits, understanding how to write loop equations is essential, especially when the direction of currents is unknown. In such cases, it is necessary to assume a direction for the currents, which can be thought of as making an educated guess. If the actual direction differs from the assumed one, the final result will indicate this through a negative current value, but the magnitude will remain accurate.

The process of writing loop equations involves several steps. First, label the positive and negative terminals of each component in the circuit. For batteries, the longer terminal is positive, while for resistors, the positive side is where the current enters. If the direction of the current is assumed, this labeling will follow that assumption. Once the terminals are labeled, the next step is to traverse the loop in the chosen direction, crossing each element and noting the voltage changes.

When crossing elements, the voltage is added if moving from negative to positive and subtracted if moving from positive to negative. This is based on Ohm's Law, which states that the voltage across a resistor can be calculated using the formula \( V = I \cdot R \), where \( V \) is voltage, \( I \) is current, and \( R \) is resistance.

For example, if you are analyzing a circuit with a 2-ohm resistor and a 4-volt battery, you would write the loop equation by summing the voltages as you traverse the loop. If you cross the resistor from positive to negative, you would subtract the voltage, resulting in a term like \( -I \cdot 2 \) for the resistor. If you cross the battery from positive to negative, you would subtract the 4 volts. The equation would then be set to zero, representing Kirchhoff's Voltage Law, which states that the sum of the electrical potential differences around any closed circuit is zero.

After setting up the equation, you can solve for the unknown current. If the calculated current is positive, it confirms that the assumed direction was correct. If it is negative, it indicates that the actual current flows in the opposite direction to what was assumed. This method allows for flexibility in circuit analysis, as the correct magnitude of current can still be determined regardless of the initial assumption.

In summary, when writing loop equations in circuits with unknown current directions, always assume a direction, label the components accordingly, and apply Kirchhoff's Voltage Law to derive the equations. This systematic approach will lead to accurate results, even if the initial assumptions about current direction are incorrect.

Solving Circuits with Multiple Sources

In analyzing electrical circuits, Kirchhoff's rules are essential for understanding current and voltage relationships. Kirchhoff's Junction Rule states that the total current entering a junction must equal the total current leaving that junction. This principle is crucial when dealing with complex circuits that have multiple branches. The Loop Rule, on the other hand, asserts that the sum of the electrical potential differences (voltage) around any closed loop in a circuit must equal zero. This means that the total voltage gained (from sources) must equal the total voltage lost (across resistors).

To effectively apply these rules, follow a systematic approach. First, label all junctions and loops in the circuit. A junction is where the circuit branches, while loops are arbitrary paths taken through the circuit. Next, assign assumed directions for the currents in each branch. It’s important to note that these assumptions can be arbitrary; if a current is calculated to be negative, it simply indicates that the actual direction is opposite to the assumed direction.

Once the circuit is labeled and currents are assigned, identify the voltage sources and resistors. For voltage sources, the longer line indicates the positive terminal, while for resistors, the current direction determines the polarity. This setup is critical because incorrect labeling can lead to erroneous results.

Next, write junction equations based on the currents at each junction. For example, if two currents enter a junction and one exits, the equation would be I₁ + I₂ = I₃. After establishing junction equations, proceed to write loop equations for each loop, ensuring that the sum of the voltages equals zero. For instance, if traversing a loop encounters a voltage source and resistors, the equation might look like: V_source - I_R = 0, where V_source is the voltage of the source and I_R is the voltage drop across the resistor calculated using Ohm's Law (V = IR).

After formulating the equations, solve for the unknown currents. If a current is found to be negative, it indicates that the assumed direction was incorrect, but the magnitude remains valid. For example, if I₂ is calculated as -0.4 A, it means the actual current flows in the opposite direction. Finally, use the junction equations to find any remaining unknown currents, ensuring that all calculations are consistent with Kirchhoff's rules.

In summary, Kirchhoff's rules provide a structured method for analyzing complex circuits. By labeling components, assigning current directions, and systematically applying the junction and loop rules, one can accurately determine the behavior of electrical circuits.

Combining Voltage Sources in Series

In electrical circuits, combining voltage sources can simplify analysis, particularly when they are connected in series. When voltage sources are in series, their voltages can be summed up. For instance, if you have a 10-volt battery and a 5-volt battery connected in series, the total voltage can be calculated as:

$$ V_{\text{total}} = V_1 + V_2 $$

In this case, the combined voltage would be 15 volts. It's important to note that if the voltage sources are oriented in opposite directions, their voltages will subtract rather than add. For example, if a 10-volt source is pushing current in one direction and a 5-volt source is pushing in the opposite direction, the effective voltage can be determined by:

$$ V_{\text{effective}} = V_1 - V_2 $$

Here, the effective voltage would be 5 volts in the direction of the stronger source.

When analyzing the circuit, the direction of current flow can be determined by the orientation of the voltage sources. If both sources are pushing current in the same direction, the current will flow clockwise. Conversely, if they oppose each other, the stronger source dictates the overall direction of current flow.

To find the magnitude of the current in a circuit, Ohm's Law is applied, which states:

$$ V = I \cdot R $$

Rearranging this gives:

$$ I = \frac{V}{R} $$

For example, with a total voltage of 15 volts and a resistance of 5 ohms, the current can be calculated as:

$$ I = \frac{15 \text{ volts}}{5 \text{ ohms}} = 3 \text{ amps} $$

In the case where the effective voltage is 5 volts against a 5-ohm resistor, the current would be:

$$ I = \frac{5 \text{ volts}}{5 \text{ ohms}} = 1 \text{ amp} $$

This approach to merging voltages and calculating current is fundamental in circuit analysis, allowing for a clearer understanding of how components interact within an electrical system.

Find Two Voltages (3 sources)

In analyzing a circuit with three batteries and three resistors, the goal is to determine the voltages \( V_1 \) and \( V_2 \) while utilizing the given voltage and currents. The process begins with labeling key components such as junctions, loops, and currents, which is essential for applying circuit laws effectively.

Junctions are points where wires split, and in this case, they are labeled as points A and B. According to the junction rule, the total current entering a junction must equal the total current leaving it. For instance, if 5 amps and 4 amps enter a junction, then 9 amps must exit, allowing us to determine all three currents in the circuit.

Next, we establish loops in the circuit to apply Kirchhoff's Voltage Law, which states that the sum of the electrical potential differences (voltages) around any closed circuit loop must equal zero. In this example, two loops are identified, and we will derive equations for each.

For the first loop, we account for the voltages as we traverse the circuit. Starting from a battery with 18 volts, we note the transitions between positive and negative terminals. The voltage across a resistor can be calculated using Ohm's Law, expressed as \( V = I \cdot R \). For the first loop, the equation can be set up as follows:

Sum of voltages: \( 18 - 40 + V_1 - 36 = 0 \)

Here, \( 40 \) volts is the voltage drop across a resistor with a current of 5 amps and resistance of 8 ohms, and \( 36 \) volts is from a resistor with a current of 9 amps and resistance of 4 ohms. Solving this equation yields:

\( V_1 = 58 \, \text{volts} \)

Next, we write the equation for the second loop, which also includes two batteries and the resistors. The equation for this loop is structured similarly:

Sum of voltages: \( V_2 - 24 + 58 - 36 = 0 \)

In this case, \( 24 \) volts is the voltage drop across a resistor with a current of 4 amps and resistance of 6 ohms. Rearranging the equation gives:

\( V_2 = 2 \, \text{volts} \)

Through this systematic approach of labeling, applying Kirchhoff's laws, and utilizing Ohm's Law, we successfully determined both \( V_1 \) and \( V_2 \), along with confirming the currents in the circuit. This methodical process is crucial for analyzing complex electrical circuits effectively.

For the circuit below, calculate 
(a) the voltage V₁ shown, and 
(b) the current through the 6-Ohm resistor.

• A. i_6Ω = 4.67 A, V₁ = 1.8 V
• B. i_6Ω = 4.67 A, V₁ = 24 V
• C. i_6Ω = 0.67 A, V₁ = 26 V
• D. i_6Ω = 0.67 A, V₁ = 30 V

Answer: (D)

For the circuit below, calculate the voltage across the 100-Ohm resistor.

• A. 10 V
• B. 17 V
• C. 24 V
• D. 56 V

Answer: (B)

How to Check Your Work (Kirchhoff's Rules)

In analyzing complex circuits, a reliable method to verify your calculations involves ensuring that all branches maintain the same voltage magnitude. This principle stems from Kirchhoff's Voltage Law, which states that the total voltage around any closed loop in a circuit must equal zero. When you have a voltage source, such as a 9-volt battery, the voltage across all components in that branch should also reflect this value, provided they are in the same loop.

To check your work, start by calculating the voltage across each resistor using Ohm's Law, expressed as \( V = I \cdot R \), where \( V \) is voltage, \( I \) is current, and \( R \) is resistance. For example, if you have a resistor with a current of 2 A and a resistance of 20 ohms, the voltage across it would be \( V = 2 \, \text{A} \times 20 \, \Omega = 40 \, \text{V} \).

Next, consider the polarity of the voltages. The direction of current flow determines the positive and negative terminals of each component. If two voltages are in opposite directions, you subtract the smaller from the larger to find the net voltage. For instance, if you have an 18 V source and a 40 V resistor in opposing directions, the net voltage would be \( 40 \, \text{V} - 18 \, \text{V} = 22 \, \text{V} \) in the direction of the larger voltage.

Continue this process for all branches in the circuit. If you find that the equivalent voltages across all branches match, your calculations are likely correct. For example, if you calculate a voltage of 22 V for multiple branches, this consistency reinforces the accuracy of your work.

In summary, by applying Kirchhoff's Voltage Law and Ohm's Law, and by carefully considering the direction of current flow, you can effectively double-check your circuit calculations. This method not only helps in confirming your results but also enhances your understanding of circuit behavior.

Here’s what students ask on this topic:

What is Kirchhoff's Loop Rule and how is it applied in circuit analysis?

Kirchhoff's Loop Rule states that the sum of all voltages around a closed loop in a circuit is zero. This principle is essential for analyzing circuits with multiple voltage sources. To apply it, you write loop equations for each loop in the circuit. Start at a point in the loop and move in a chosen direction (clockwise or counterclockwise), adding or subtracting voltages based on the direction of the current and the loop. For resistors, use Ohm's Law ($V=IR$) to find voltage drops. The sum of these voltages should equal zero.

How do you determine the direction of current and loop in Kirchhoff's Loop Rule?

The direction of the current is usually given or assumed based on the circuit's configuration. For resistors, the positive end is where the current enters. For batteries, the positive terminal is fixed. When choosing the loop direction, you can go clockwise or counterclockwise. The key is consistency: if you cross an element from negative to positive, you add its voltage; if from positive to negative, you subtract it. The direction of the loop does not affect the final equation, as it will yield the same result regardless of the chosen direction.

How do you combine voltage sources in series using Kirchhoff's Loop Rule?

Voltage sources in series can be combined to simplify a circuit. If the sources are aligned in the same direction, their voltages add up. If they are in opposite directions, their voltages subtract. For example, a 10V and a 5V battery in series with the same polarity will combine to a single 15V source. If they are opposing, the effective voltage will be 10V - 5V = 5V. This simplification helps in writing loop equations and analyzing the circuit more easily.

How can you verify your circuit analysis using Kirchhoff's Loop Rule?

To verify your circuit analysis, ensure that all branches have consistent voltage magnitudes and polarities. Check that the sum of voltages around each loop equals zero. Use Ohm's Law ($V=IR$) to calculate voltage drops across resistors. Compare the calculated voltages with the known values to ensure they match. This double-checking process helps identify any mistakes in your calculations and ensures the accuracy of your analysis.

What are common mistakes to avoid when applying Kirchhoff's Loop Rule?

Common mistakes include incorrect assignment of voltage polarities, inconsistent loop direction, and errors in applying Ohm's Law. Always ensure that the positive end of a resistor is where the current enters and that the positive terminal of a battery is correctly identified. Be consistent with the loop direction throughout the analysis. Double-check your calculations for voltage drops using $V=IR$. These steps help avoid errors and ensure accurate results.