Combining Resistors in Series & Parallel - Online Tutor, Practice Problems & Exam Prep

Understanding how to combine resistors is essential in circuit analysis. Resistors can be connected in series or parallel. In series, the equivalent resistance (R_eq) is the sum of individual resistances: R = R₁+R₂+R₃. In parallel, the equation is more complex: 1Rₑquivalence = 1R₁+1R₂. Shortcuts exist for two resistors in parallel, allowing for quicker calculations. Combining resistors effectively simplifies circuit analysis and enhances understanding of electrical resistance.

Combining Resistors in Series & Parallel

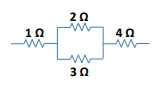
Hey guys. So in this video, we're going to talk about combining resistors, which is a key skill that you have to master for this chapter. Let's go. Alright. So in circuit problems, you're often going to be asked to collapse or combine or merge multiple resistors into a single equivalent resistor. Single equivalent resistor, just one. And resistors can be connected to each other in two ways. They can be connected in series or in parallel. And this looks like this. In series, you're going to have resistors sort of side by side like this. In parallel, you're going to have resistors like this. Alright? And what you want to do is you want to go from a number of multiple resistors, let's say here three, into a single equivalent resistor. Same thing here. You want to turn these three resistors into just a single resistor. Now what makes this a series connection is that you have a direct connection between the resistors without any splits in the wire. So imagine if you are an electron traveling through this wire, you go straight through with no forks on the rope. Alright? So and then here the wire splits and because the wire splits you get some loops. So let's say we connect this to let's connect this to a battery, to a voltage source kind of like a battery. Right? Remember, charge moves out of the current is going to flow out of the positive, the larger terminal here. It's going to go this way. When it gets here, it has the choice of moving this way or this way. So some of the charge will go one way, some of the charge will go the other way. So the wire splits and a forms of loop. So one other thing that's important to note is you have a parallel connection whenever you have two resistors that are alone on opposite pay on opposite sides, on opposite branches. So let me write this, alone on opposite opposite branches. We're opposite sides. You can think of it that way as well. So for example, this guy is alone in this branch. This guy is alone in this branch. So they are alone on opposite sides or on opposite branches. Therefore, they are in parallel. Alright? Now the way you combine them is by using the equivalent resistance equation which is different for series and parallel and you have to memorize this one. The equivalent resistance if you're in series is just the addition of the individual resistances, r_one+r_two+r_three. For example, if this is a 1 ohm resistor and this one's 2 and this one's 3, this equivalent resistor here is going to be 6. You just add up the numbers.

Now if you are in parallel, the equation is a little bit more complicated. It's 1/r_equivalence=1/r_one+1/r_two+…+1/r₃. Here I have three, so I'm going to write 1/r₃. Okay? And what it means to be an equivalent resistor is that you behave the same as the original group of resistors. So let me illustrate this. Let's connect the battery here, positive, side of the battery. So the current is going to flow out this way. The idea is that this group of resistors, this group of resistors, behaves just as this single resistor would here. As far as the battery is concerned, it is the same exact thing. The battery cannot distinguish these three resistors from a single equivalent resistor, which is why they're called equivalents. Same thing here. If you combine these three resistors into a single equivalent resistor, as far as the battery is concerned, the battery sees the same exact amount of resistance.

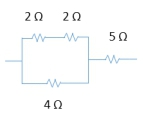
One last point I want to make is that if you combine resistors in series like we did here, the equivalent resistance is always going to be higher than the individual resistances. And this should make sense since you're adding the numbers, right, 1 plus 2 plus 3, the total number is obviously going to be higher. Now if you have a parallel connection, the number is always going to be lower. And that's because in this case, remember I mentioned that the current splits, so now because the electrons have an option of going one way or the other, there's effectively less resistance because they have a choice. Cool? So let's do two examples here. What is the equivalent resistance of the resistance of the following resistors? What we want to do is get from 4 resistors into a single resistor. And there are, sometimes there are multiple ways of doing this, multiple paths that you can take to get to the answer. Sometimes there's only one path. And what you have to sort of do is map out how are you going to go from 4 to 1. And what you want to do is look for places where you can easily combine these resistors. So for example, one thing you might do is look at 1 and start comparing it and start seeing how it's connected to every single one of these. So is 1 in series or in parallel with 2? Well, remember series means that they have a direct connection. Is there a direct connection from 1 to 2? So if you're a charge, you're going through here. And then right here, the wire splits. There is no direct connection. So 1 and2

What is the equivalent resistance of the following combination of resistors?

• A. 0.69 Ω
• B. 1.45 Ω
• C. 5.8 Ω
• D. 6.2 Ω

Shortcut Equations for Resistors Parallel

Hey guys. So in this video, I'm going to show you some awesome shortcuts that you can use in some cases when you have resistors in parallel. And this is going to keep you from having to do a lot of work with fractions. Let's check it out. All right, so if you have 2 resistors in parallel, there's a shortcut equation you can use. Now remember, the general equation is that the equivalent resistance in parallel is req=1r+1r1+1r2. This is if you have 2 resistors, this is the general equation. K? And I'm going to solve for requiv so that you never have to do this again. And you can just use a shortcut if you have 2 resistors, which is the most common thing you're going to get. So the first thing if you remember we have to do is get a common denominator. And to do that, you're just going to multiply r2 here and then multiply r1 here. So r1×r2. So if I do in the bottom, I also have to do it in the top r2×r1×r1. Let's extend the little fraction thing. So what happens now is I have r1×r2 at the bottom, so I have a common denominator so I can write r1×r2. And then at the top I have r2+r1, or I'm going to write it r1+r2. So it's in order. Are we done? No. Remember we have to flip the sides. So if I flip here, I get requiv=r1×r2,r1+r2. Now notice I'm drawing the r1 and r2 in the bottom really far apart and the reason I'm doing this is because one of the biggest problems with this equation is that people forget whether the times is on top or the plus is on top. You don't know what goes where, you might forget. The way I remember, which is silly but works is because this is a dot, it's a tiny dot. The r1 and r2 are really close together and this is a fat plus sign, which takes up a lot more space. The bottom variables are farther apart and the skinny top and fat bottom gives you sort of a triangle. K. Super silly but maybe hopefully it works for you. Whatever works. Right? So that's the equation. So whenever you have 2 resistors in parallel, you can just use that equation instead of playing with fractions. K? Now super important is that you cannot do this for 3 or more resistors. So I actually want you to draw write this here. This is wrong, but I want you to write it. Let's say you might wanna think that you can multiply r1,r2, why not just add an r3 here, and then at the bottom here, do a plus r3. Well, this is wrong. This does not work. So I want you to write it, scratch it out and say don't. K? Do not do this. This only works for 2 resistors. It does not work for more than 2. Okay? So let me give you a super quick example here. Let's say you have a 4 and a 6 and you want to combine them into a single resistor, you would just use this equation here and say that the equivalent resistance is 4×6 divided by 4+6. I'm setting up the parenthesis so I can put the numbers inside. 4, and 6, and this is 24 divided by 10, which is 2.4. Right? Much faster than play with fractions. So that's the first shortcut. The most important thing always is that you know the general equation because this is going to work for everything, but this shortcut is pretty handy as well. It's more important shortcut number 2, but shortcut number 2 is super simple. If you have resistors of the same resistance, you can also use a shortcut equation. So let's say I have a, let's make it creepy. 666. Let's say you have something like this. What's the equivalent resistance? Well, if you write the general equation, remember, you cannot write this equation right here, the one we just talked about because that works only for 2. But if you have this, you end up with something like this, 1r6+1r6+1r6. And the denominator is already the same, so you end up with 3r6 or r63, which is true. The fast way to have done this is to just say that the equivalent resistance 8, and 8, the equivalent resistance here is super easy to calculate. It's 2. Cool? So now I'm going to do an example that sort of merges all these ideas. You now know how to easily combine things that are the same and you know how to easily combine when they're the same resistance and you know how to easily combine if there's 2 of them using that first equation. Now you can actually use those two rules to your advantage. So if you get a question like this, this might look hairy, but it's actually really simple. So what we're going to do, notice we have a 9, a 9, and a 9. And even though they're not right next to each other, you could technically rearrange them to be right next to each other. And you can say, you know what? This 9 with this 9 and this 9 because they're the same, I can write the equivalent resistance of the 3 nines is just 93. I'm using this shortcut right here. There are 3 nines, so it's just 9 divided by 3, which is 3. K? You can do the same thing for the twelves. There's 2 twelves. So I can say the equivalent resistance of the twelves combined are going to be 122, just 6. So what I can do is all the reds become a simple, a single 3 and the and the blue becomes a 6. And now if I combine these 2 because I have 2 resistors that are parallel to each other. Right? Let's put the little connectors this way. So there's 2 resistors here, they are parallel to each other. I can use the first shortcut equation, which is you multiply at the top and then you add at the bottom. Remember the pyramid, right? It's multiply, and add. So this is going to be 3×6,3+6. 3×6, of course, is 18. 3+6 is 9. So the answer here is 2Ω. So notice how we're able to combine everything really, really quickly. 9,9,9,3,12 is a 6. Put them together and you get a 2Ω. Alright? That's it for this one. Let's keep going.

What is the equivalent resistance of the following combination of resistors?

• A. 0.4 Ω
• B. 2.5 Ω
• C. 7.0 Ω
• D. 10 Ω

Weird Arrangement (Re-Drawing Resistors)

Hey guys. So in this video, I want to go over an example of a network of resistors that looks scarier than it really is. So here we want to find the equivalent resistor of these guys, and it looks really hairy, but I want to show you how you can make it look more familiar to solve this question. Okay. And the key thing we're going to do here is we're going to move the wires around, so that they look more familiar. So for example, the 5 and the 4 are sort of end up at an angle, which is unusual, and it doesn't make it harder to sort of visualize what's really going on here. So the first thing I'm going to do is I'm going to try to make this 4 vertical, and I can actually just move this point here where the 3 of them, 3 wires touch. I can move this point right here, and then imagine if you have a 4 and then you're grabbing the bottom. Right? You're grabbing the bottom and just doing this. K? So if I do that, let's redraw. I'm going to get a 2 at the top, a 3 here, and then this red point right here is now going to be right here. So that I get a 4 like this and then there's still a 5 here. Let's leave that alone. We'll take this slowly. And now this hopefully looks, more familiar. The other thing we can do is notice that this is a single branch right here. That's all along this green line. There are no points where the wire splits. Now obviously, the wire splits here and the green dot splits in the red dot, but within those two dots, nothing splits. What that means is that you can actually move the 3 and just redraw the 3 over here and it's exactly the same thing. It functions just the same. So now we get something a little cleaner. And I'm going to draw again. I'm going really slowly, because I want to make sure you fully understand this. K? And now it looks like this. And hopefully, now this looks super familiar. Hopefully, you'd see that this is a branch with a single resistor in it. And this is a branch here also with a single resistor on it or in it. And because you have 2 resistors on opposite sides, they're alone on opposite sides of this loop here, they are in parallel. So these 2 guys are in parallel so I can combine them. K? Usually, I would keep going, but just just for the sake, of just getting this over with, let's just combine these 2 real quick. And because I have 2 resistors in parallel, I can use the shortcut equation. The equivalent resistance is going to be remember the pyramid, it's of times on top and plus on the bottom. Okay? So it's going to be 4×34+3 which is 12/7, which is approximatley 1.7 ohms. K? So this entire thing can be redrawn as all of this. Right? Can be redrawn. There's a 2, there's a 5, and instead of having a 4 and then a 3, I'm just going to have a single 1.7 right here. And now, this is a little simpler because I have 3 on top a little bit and then I'm going to move the bottom a little bit. And then I'm going to move the bottom a little bit. So I'm going to move the top a little bit and then I'm going to move the bottom a little bit. So really slowly here, the 5 is going to be moved over here and this part of the 5 is going to be moved over here so that it forms sort of a straight line. And this is going to look like this. Got a 2 and then you got a 5 straight down and then there's still the 1.7 over here. Now the 1.7 is kind of like this. Right? If you curve the 1.7, it's kind of straight like this. I can extend this wire and make it look like this. K? All these are equivalent. You just have to be careful to redraw them correctly. Otherwise, you made up a new circuit, and obviously, it's going to be wrong. K? Again here, hopefully, you see that you have a branch with a single resistor. And then here, you have a branch with a single resistor. And because you have 2 resistors that are alone on their branches, on their opposite sides, they are also in parallel. And once again, I can use the parallel shortcut equation because I have 2 resistors. The equivalent resistance is going to be 5×1.75+1.7 K? And if you do this in a calculator, you get approximately 1.31 ohms. I want to quickly remind you of something that we talked about, earlier, which is whenever you combine things in parallel, the total resistance is smaller or lower than all of the resistances. So it's going to be lower than the 5 and it's going to be lower than the 1.7. Notice that when I merge them, I got a 1.3 lower than 1.7. It makes sense. You can use that to validate that you're probably correct. So finally here, I can draw the 2 and then this entire thing here gets replaced instead of there being 2 of them, there's going to be just a single one point three and these are the points that we have there. Now notice that EIF

If every resistor below has resistance R, what is the equivalent resistance of the combination, in terms of R?

• A. 0.5R
• B. R
• C. 4R
• D. 5R

Here’s what students ask on this topic:

How do you calculate the equivalent resistance of resistors in series?

To calculate the equivalent resistance of resistors in series, you simply add their resistances together. The formula is:

$R_{\mathrm{eq}}=R_1+R_2+R_3+...+R_n$

For example, if you have three resistors with resistances of 2Ω, 3Ω, and 5Ω, the equivalent resistance would be:

$R_{\mathrm{eq}}=2+3+5=10\Omega$

What is the formula for calculating the equivalent resistance of resistors in parallel?

The formula for calculating the equivalent resistance of resistors in parallel is:

$\frac{1}{R_{\mathrm{eq}}}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+...+\frac{1}{R_n}$

For example, if you have three resistors with resistances of 2Ω, 3Ω, and 6Ω, the equivalent resistance would be:

$\frac{1}{R_{\mathrm{eq}}}=\frac{1}{2}+\frac{1}{3}+\frac{1}{6}$

After finding a common denominator and summing the fractions, you would get:

$\frac{1}{R_{\mathrm{eq}}}=\frac{6}{6}=1$

So, $R_{\mathrm{eq}}=1\Omega$.

What is the shortcut for calculating the equivalent resistance of two resistors in parallel?

The shortcut for calculating the equivalent resistance of two resistors in parallel is:

$R_{\mathrm{eq}}=\frac{R_1\times R_2}{R_1+R_2}$

For example, if you have two resistors with resistances of 4Ω and 6Ω, the equivalent resistance would be:

$R_{\mathrm{eq}}=\frac{4\times 6}{4+6}=\frac{24}{10}=2.4\Omega$

How do you combine resistors of the same resistance in parallel?

When combining resistors of the same resistance in parallel, you can use a simple shortcut. If you have $n$ resistors, each with resistance $R$, the equivalent resistance is:

$R_{\mathrm{eq}}=\frac{R}{n}$

For example, if you have three resistors, each with a resistance of 6Ω, the equivalent resistance would be:

$R_{\mathrm{eq}}=\frac{6}{3}=2\Omega$

Why is the equivalent resistance of resistors in parallel always lower than the smallest individual resistance?

The equivalent resistance of resistors in parallel is always lower than the smallest individual resistance because the current has multiple paths to flow through. This effectively reduces the overall resistance. When resistors are in parallel, the total current is divided among the parallel branches, making it easier for the current to flow. Mathematically, this is represented by the formula:

$\frac{1}{R_{\mathrm{eq}}}=\frac{1}{R_1}+\frac{1}{R_2}+...+\frac{1}{R_n}$

Since the reciprocal of the equivalent resistance is the sum of the reciprocals of the individual resistances, the equivalent resistance is always less than the smallest individual resistance.