Systems of Objects on Inclined Planes with Friction: Videos & Practice Problems

In problems involving connected systems, inclined planes, and friction, it's essential to identify the type of friction—static or kinetic. For example, when analyzing two blocks on a 30-degree incline, draw free body diagrams to visualize forces like weight, normal force, tension, and kinetic friction. Use Newton's second law, F = m × a, to set up equations for each block, considering the direction of acceleration. Solving these equations reveals the system's acceleration, integrating concepts of force, friction, and motion effectively.

Connected Objects On Inclined Planes With Friction

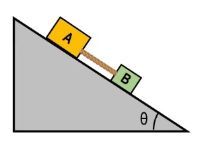
In solving problems involving connected systems of objects, inclined planes, and friction, it is essential to integrate these concepts effectively. When approaching such problems, the type of friction—static or kinetic—will typically be specified in the problem statement. This clarity allows for a more straightforward application of the problem-solving steps previously learned.

Consider a scenario with two blocks on a 30-degree inclined plane, where one block (Block A) is on the incline and the other (Block B) is hanging. The known parameters include the weights and masses of both blocks, as well as the coefficient of kinetic friction. Since Block B is moving up the incline, we can conclude that kinetic friction is acting on Block A, opposing its motion.

To analyze the forces acting on each block, we begin by drawing free body diagrams. For Block A, the forces include its weight (\(m_A g\)), the normal force perpendicular to the surface, tension from the cable, and kinetic friction. The weight can be resolved into components along the incline, with \(m_A g \sin(\theta)\) acting down the incline and \(m_A g \cos(\theta)\) acting perpendicular to it. For Block B, the forces consist of its weight (\(m_B g\)) acting downward and the tension in the cable acting upward.

Next, we apply Newton's second law, \(F = ma\), to each block. For Block B, the equation can be expressed as:

\[ \sum F_y = m_B g - T = m_B a \]

For Block A, the forces along the incline yield:

\[ \sum F_x = T - m_A g \sin(\theta) - f_k = m_A a \]

Here, \(f_k\) represents the kinetic friction, calculated as \(f_k = \mu_k N\), where \(N\) is the normal force. On an incline, the normal force is given by \(N = m_A g \cos(\theta)\). Thus, the kinetic friction can be expressed as:

\[ f_k = \mu_k m_A g \cos(\theta) \]

By substituting known values into these equations, we can solve for the unknowns, which include the tension and the acceleration of the system. After setting up the equations and eliminating the tension, we can find the acceleration by combining the equations appropriately. The final result for the acceleration of the system can be calculated, yielding a value of \(5.2 \, \text{m/s}^2\).

This process illustrates the importance of systematically applying the principles of mechanics to solve complex problems involving multiple forces and motion on inclined planes. Understanding the interactions between these forces is crucial for accurately determining the behavior of the system.

Two blocks made of different materials, connected by a string, slide down a 30° inclined plane. Block A has mass 8kg, and the coefficient of kinetic friction between Block A and the incline is 0.35. Block B has mass 4kg, and the coefficient of friction between block B and the plane is 0.25. After the blocks are released, find the tension in the cord.

• A. 1.23 N
• B. 2.21 N
• C. 1.67 N
• D. 2.28 N

Answer: (D)

Blocks on a Wedge

In this problem, we analyze a system of two blocks connected on inclined planes, considering the effects of gravity and friction to determine the system's acceleration. The setup involves two blocks, one with a mass of 5 kg on a steeper incline and another with a mass of 2 kg on a shallower incline. To solve for the acceleration, we start by drawing free body diagrams for each block, identifying the forces acting on them, including weight, tension, normal force, and friction.

For block A (5 kg), the weight force acts downward, while the tension force points up the incline. The friction force's direction is initially uncertain, but since the system begins to move, we deduce that the friction must act down the ramp. The gravitational force can be decomposed into components: the parallel component is given by \( m_A g \sin(\theta_A) \) and the perpendicular component by \( m_A g \cos(\theta_A) \). The friction force is calculated using the coefficient of kinetic friction \( \mu_k \) and the normal force, leading to \( f_k = \mu_k m_A g \cos(\theta_A) \).

For block B (2 kg), the analysis is similar, with the weight force acting downward and the tension pointing in the opposite direction. The friction force here acts up the incline. The equations for the forces can be expressed as follows:

For block A:

\[ T - m_A g \sin(\theta_A) - f_k = m_A a \]

For block B:

\[ m_B g \sin(\theta_B) - T - f_k = m_B a \]

Substituting the expressions for the friction force and simplifying leads to two equations that can be solved simultaneously. After substituting known values and simplifying, we find:

1. From block A: \( T - 8.86 = 2a \)

2. From block B: \( 16.01 - T = 5a \)

By adding these equations, the tension cancels out, allowing us to solve for acceleration:

\[ 7.15 = 7a \]

Thus, the acceleration \( a \) is calculated as:

\[ a = 1.02 \, \text{m/s}^2 \]

This result indicates the magnitude of the system's acceleration, confirming that the system accelerates in the expected direction. The final answer aligns with the problem's requirements, providing a clear understanding of the dynamics involved in the system of blocks on inclined planes.

Here’s what students ask on this topic:

How do you determine the type of friction acting on a system of objects on an inclined plane?

To determine the type of friction acting on a system of objects on an inclined plane, you need to analyze the problem text. The problem will usually specify whether the friction is static or kinetic. Static friction occurs when the objects are not moving relative to each other, while kinetic friction occurs when there is relative motion between the objects. For example, if the problem states that a block is moving up an incline, you are dealing with kinetic friction. Identifying the type of friction is crucial for setting up the correct equations to solve the problem.

What are the steps to solve a problem involving connected systems on inclined planes with friction?

To solve a problem involving connected systems on inclined planes with friction, follow these steps: 1) Draw free body diagrams for each object to visualize forces like weight, normal force, tension, and friction. 2) Identify the type of friction (static or kinetic) from the problem text. 3) Use Newton's second law, $F=m\times a$, to set up equations for each object, considering the direction of acceleration. 4) Solve the system of equations to find the unknowns, such as acceleration and tension. This method integrates concepts of force, friction, and motion effectively.

How do you draw free body diagrams for objects on an inclined plane with friction?

To draw free body diagrams for objects on an inclined plane with friction, follow these steps: 1) Identify all forces acting on the object, including weight (mg), normal force (perpendicular to the surface), tension (if connected by a cable), and friction (opposing motion). 2) Represent the weight force as a vector pointing straight down. 3) Draw the normal force perpendicular to the inclined plane. 4) Include the tension force along the direction of the cable. 5) Add the friction force opposing the direction of motion. 6) Tilt the coordinate system to align with the incline, breaking the weight force into components parallel and perpendicular to the plane.

How do you use Newton's second law to solve for acceleration in a system of objects on an inclined plane with friction?

To use Newton's second law to solve for acceleration in a system of objects on an inclined plane with friction, follow these steps: 1) Write the equation $F=m\times a$ for each object. 2) For each object, sum the forces in the direction of motion and set them equal to the mass times acceleration. 3) Include forces such as tension, weight components, normal force, and friction. 4) Solve the equations simultaneously to find the unknowns, such as acceleration and tension. This method allows you to determine the system's acceleration by integrating the effects of all forces involved.

What is the role of the normal force in problems involving inclined planes with friction?

The normal force plays a crucial role in problems involving inclined planes with friction. It acts perpendicular to the surface of the inclined plane and is responsible for balancing the perpendicular component of the weight force. The normal force is also essential for calculating frictional forces, as friction is proportional to the normal force. For kinetic friction, the frictional force is given by $f$_k = μ_k N, where $\mu$_k is the coefficient of kinetic friction and $N$ is the normal force. Understanding the normal force helps in accurately determining the frictional forces and solving the problem.