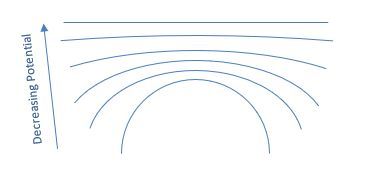
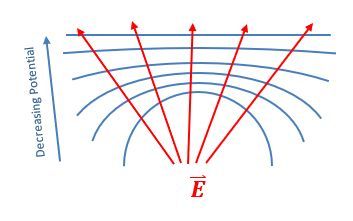
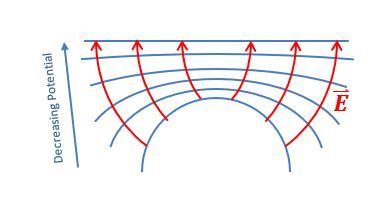
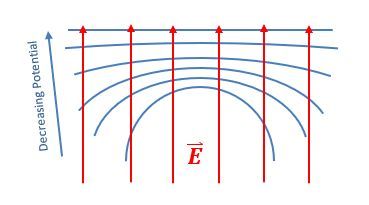
Equipotential surfaces are regions in space where the electric potential is constant. The term "equipotential" combines "equi," meaning equal, and "potential," referring to electric potential. This means that along these surfaces, the change in potential, denoted as ΔV, is zero. For a point charge, the electric potential can be expressed with the formula:
\[ V = \frac{kQ}{r} \]
where \( k \) is Coulomb's constant, \( Q \) is the charge, and \( r \) is the distance from the charge. If you consider a point charge and measure the potential at a constant distance \( r \), you will find that all points along this distance form a circle, representing an equipotential surface. For example, if the potential is 10 volts, all points on this circle will have the same potential.
There are infinitely many equipotential surfaces corresponding to different potential values, such as 5 volts, 10 volts, and 20 volts. The relationship between electric fields and potential is crucial; the electric field \( E \) can be defined as:
\[ E = -\frac{ΔV}{Δx} \]
or equivalently:
\[ ΔV = -E \cdot Δx \]
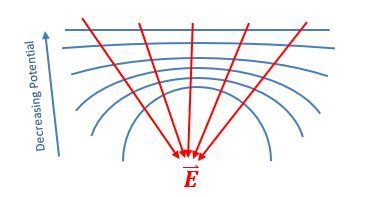
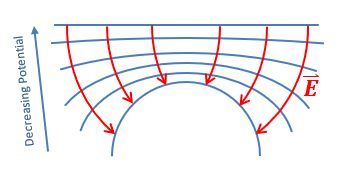
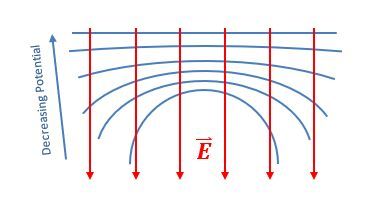
Electric field lines are always perpendicular to equipotential surfaces. This means that if you have an equipotential surface, the electric field will point in a direction that is at a right angle to that surface. Additionally, electric field lines point from regions of higher potential to lower potential. For a positive point charge, as you move away from the charge, the potential decreases, which is why the electric field lines radiate outward.
When considering electric dipoles, which consist of a positive and a negative charge, the equipotential surfaces take on a different shape. The electric field lines between the two charges curve, and the equipotential surfaces are straight lines perpendicular to these field lines at the midpoint. As you approach either charge, the equipotential surfaces become more distorted due to the influence of the nearby charge.
It's also important to note that the work done in moving a charge along an equipotential surface is zero because the potential difference (ΔV) is zero. However, moving a charge between different equipotential surfaces requires work, as it involves overcoming the electric field.
To illustrate this concept, consider a point charge of 1 microcoulomb and an equipotential surface of 150 volts. Using the potential formula, we can find the distance \( r \) from the charge to the equipotential surface:
\[ r = \frac{kQ}{V} \]
Substituting the values, where \( k \) is approximately \( 8.99 \times 10^9 \, \text{N m}^2/\text{C}^2 \), \( Q = 1 \times 10^{-6} \, \text{C} \), and \( V = 150 \, \text{V} \), we find:
\[ r = \frac{8.99 \times 10^9 \times 1 \times 10^{-6}}{150} \approx 60 \, \text{m} \]
This means that at a distance of 60 meters from the point charge, the potential will be 150 volts along the equipotential surface.