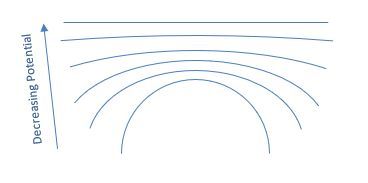
Equipotential Surfaces: Videos & Practice Problems

Equipotential surfaces are regions where electric potential remains constant, meaning that the potential difference (ΔV) is zero. For a point charge, these surfaces appear as concentric circles. The electric field (E) is always perpendicular to these surfaces and points in the direction of decreasing potential. For electric dipoles, equipotential surfaces take on a more complex shape, often resembling straight lines near the center. The work done in moving a charge along an equipotential surface is zero, while moving between different surfaces requires work against the electric field. The equation for electric potential is given by V = kqr.

Equipotential Surfaces

Equipotential surfaces are regions in space where the electric potential is constant. The term "equipotential" combines "equi," meaning equal, and "potential," referring to electric potential. This means that along these surfaces, the change in potential, denoted as ΔV, is zero. For a point charge, the electric potential can be expressed with the formula:

$$ V = \frac{kQ}{r} $$

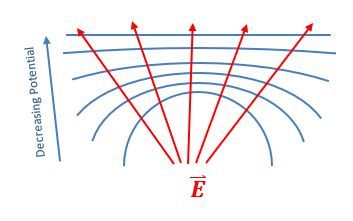
where \( k \) is Coulomb's constant, \( Q \) is the charge, and \( r \) is the distance from the charge. If you consider a point charge and measure the potential at a constant distance \( r \), you will find that all points along this distance form a circle, representing an equipotential surface. For example, if the potential is 10 volts, all points on this circle will have the same potential.

There are infinitely many equipotential surfaces corresponding to different potential values, such as 5 volts, 10 volts, and 20 volts. The relationship between electric fields and potential is crucial; the electric field \( E \) can be defined as:

$$ E = -\frac{ΔV}{Δx} $$

or equivalently:

$$ ΔV = -E \cdot Δx $$

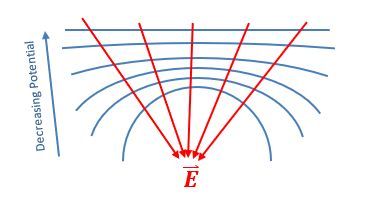
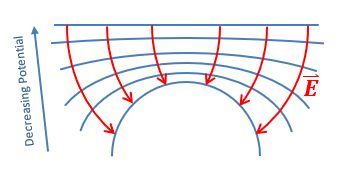
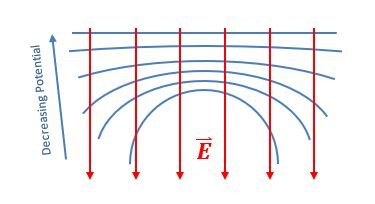
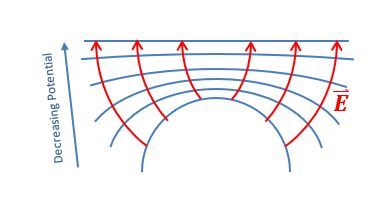
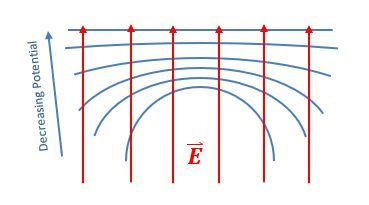
Electric field lines are always perpendicular to equipotential surfaces. This means that if you have an equipotential surface, the electric field will point in a direction that is at a right angle to that surface. Additionally, electric field lines point from regions of higher potential to lower potential. For a positive point charge, as you move away from the charge, the potential decreases, which is why the electric field lines radiate outward.

When considering electric dipoles, which consist of a positive and a negative charge, the equipotential surfaces take on a different shape. The electric field lines between the two charges curve, and the equipotential surfaces are straight lines perpendicular to these field lines at the midpoint. As you approach either charge, the equipotential surfaces become more distorted due to the influence of the nearby charge.

It's also important to note that the work done in moving a charge along an equipotential surface is zero because the potential difference (ΔV) is zero. However, moving a charge between different equipotential surfaces requires work, as it involves overcoming the electric field.

To illustrate this concept, consider a point charge of 1 microcoulomb and an equipotential surface of 150 volts. Using the potential formula, we can find the distance \( r \) from the charge to the equipotential surface:

$$ r = \frac{kQ}{V} $$

Substituting the values, where \( k \) is approximately \( 8.99 \times 10^9 \, \text{N m}^2/\text{C}^2 \), \( Q = 1 \times 10^{-6} \, \text{C} \), and \( V = 150 \, \text{V} \), we find:

$$ r = \frac{8.99 \times 10^9 \times 1 \times 10^{-6}}{150} \approx 60 \, \text{m} $$

This means that at a distance of 60 meters from the point charge, the potential will be 150 volts along the equipotential surface.

Field due to Equipotential Surfaces

Equipotential surfaces are crucial in understanding electric fields, as they help visualize how electric potential varies in space. When analyzing these surfaces, it's essential to remember two key principles: the electric field lines are always perpendicular to equipotential surfaces, and they point in the direction of decreasing potential.

To determine the direction of the electric field, consider the angle formed with the axes. For instance, if the electric field makes a 60-degree angle with the x-axis, the electric field will point 30 degrees below the negative x-axis, due to the perpendicular relationship between the electric field and the equipotential surfaces.

To calculate the magnitude of the electric field (\(E\)), we use the formula:

\(E = -\frac{\Delta V}{\Delta x}\)

In this equation, \(\Delta V\) represents the change in electric potential, and \(\Delta x\) is the distance over which this change occurs. For example, if the potential difference between two equipotential surfaces is 5 volts and the spacing between them is 1 centimeter (0.01 meters), we can substitute these values into the equation:

\(E = -\frac{5 \, \text{V}}{0.01 \, \text{m}} = -500 \, \text{V/m}\)

This result indicates a constant electric field magnitude of 500 volts per meter. It's important to note that the unit of volts per meter can also be expressed as newtons per coulomb, providing an alternative perspective on the electric field's strength.

In summary, to analyze electric fields due to equipotential surfaces, identify the potential differences and spacings, determine the direction of the electric field towards decreasing potentials, and apply the formula for magnitude. This systematic approach will yield a comprehensive understanding of the electric field in relation to equipotential surfaces.

Draw the electric field that corresponds to the equipotential surfaces shown in the following figure. Note that the potential is decreasing in the upward direction.

• A.
• B.
• C.
• D.
• E.
• F.

Answer: (E)

Here’s what students ask on this topic:

What are equipotential surfaces in physics?

Equipotential surfaces are regions in space where the electric potential is constant. This means that the potential difference (ΔV) between any two points on the surface is zero. For a point charge, these surfaces appear as concentric circles centered around the charge. The electric field (E) is always perpendicular to these surfaces and points in the direction of decreasing potential. Equipotential surfaces are useful in visualizing electric fields and understanding the work done in moving charges within an electric field.

How do equipotential surfaces relate to electric fields?

Equipotential surfaces are always perpendicular to electric field lines. The electric field (E) points in the direction of decreasing potential, meaning it is perpendicular to the equipotential surfaces. This relationship can be expressed by the equation $E=\frac{-\mathrm{\Delta V}}{\mathrm{\Delta x}}$. This perpendicularity helps in visualizing the direction and strength of the electric field. Additionally, no work is required to move a charge along an equipotential surface, as ΔV is zero.

What is the significance of equipotential surfaces in electric dipoles?

In electric dipoles, equipotential surfaces take on more complex shapes compared to point charges. Near the center of a dipole, these surfaces often resemble straight vertical lines. This is because the electric potential from the positive and negative charges cancels out along these lines. As you move closer to one of the charges, the equipotential surfaces become more curved. Understanding these surfaces helps in visualizing the electric field and potential distribution around dipoles, which is crucial for solving problems involving dipole interactions.

Why is no work required to move a charge along an equipotential surface?

No work is required to move a charge along an equipotential surface because the potential difference (ΔV) along the surface is zero. The work done (W) in moving a charge (q) is given by the equation $W=q\mathrm{\Delta V}$. Since ΔV is zero on an equipotential surface, the work done is also zero. This property simplifies calculations and helps in understanding the behavior of charges in electric fields.

How do you calculate the distance to an equipotential surface for a point charge?

To calculate the distance (r) to an equipotential surface for a point charge, you can use the equation for electric potential $V=\frac{kq}{r}$. Rearrange this equation to solve for r: $r=\frac{kq}{V}$. For example, if you have a 1 μC point charge and want to find the distance to an equipotential surface of 150 V, you would calculate $r=\frac{8.99\times 10^9\times 1\times 10^-6}{150}=60m$.