Gauss' Law: Videos & Practice Problems

Gauss's Law establishes a direct relationship between electric flux and enclosed charge, stating that the net flux through a closed surface is proportional to the charge within it. The equation is Φnet = Qε₀. This principle simplifies calculations of electric fields and flux, allowing for straightforward problem-solving in electrostatics, including determining flux from charge and vice versa, as well as deriving electric field equations for point charges using symmetric Gaussian surfaces.

Gauss' Law

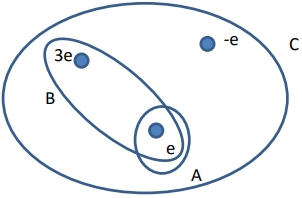
Gauss's Law is a fundamental principle in electricity that establishes a direct relationship between electric flux and charge. It states that the net electric flux through a closed surface is proportional to the total charge enclosed within that surface. This relationship can be expressed mathematically as:

$$\Phi_{\text{net}} = \frac{Q_{\text{enclosed}}}{\varepsilon_0}$$

Here, $$\Phi_{\text{net}}$$ represents the net electric flux, $$Q_{\text{enclosed}}$$ is the total charge within the closed surface, and $$\varepsilon_0$$ (epsilon naught) is the permittivity of free space, approximately equal to $$8.85 \times 10^{-12} \, \text{C}^2/\text{N} \cdot \text{m}^2$$.

To apply Gauss's Law effectively, it is essential to understand the three main types of problems that can arise:

1. **Calculating Flux from Charge**: When given a set of charges, you can determine the net flux through a surface by summing the enclosed charges. For example, if you have a positive charge of 5 C and a negative charge of 3 C within a closed surface, the total enclosed charge is 2 C. Using Gauss's Law, the net flux can be calculated as:

$$\Phi_{\text{net}} = \frac{2 \, \text{C}}{8.85 \times 10^{-12} \, \text{C}^2/\text{N} \cdot \text{m}^2} \approx 2.26 \times 10^{11} \, \text{N} \cdot \text{m}^2/\text{C}$$

2. **Finding Charge from Flux**: In some scenarios, you may be provided with the net flux and asked to find the enclosed charge. For instance, if the net flux through a closed surface is 23 N·m²/C, you can rearrange Gauss's Law to solve for the enclosed charge:

$$Q_{\text{enclosed}} = \Phi_{\text{net}} \cdot \varepsilon_0$$

By substituting the values, you can determine the total charge within the surface.

3. **Calculating Electric Field from Charge**: When tasked with finding the electric field due to a point charge, Gauss's Law can also be utilized. The electric field (E) at a distance (R) from a point charge can be derived by selecting an appropriate Gaussian surface, typically a sphere for point charges. The electric field can be expressed as:

$$E = \frac{Q_{\text{enclosed}}}{4 \pi R^2 \varepsilon_0}$$

Recognizing that $$\frac{1}{4 \pi \varepsilon_0}$$ is the constant K, the equation simplifies to:

$$E = K \frac{Q_{\text{enclosed}}}{R^2}$$

This confirms the established formula for the electric field around a point charge, demonstrating the utility of Gauss's Law in various contexts.

Understanding Gauss's Law and its applications is crucial for solving problems related to electric fields and flux, providing a powerful tool for analyzing electrostatic situations.

Electric Field Within Spherical Conductor

In this discussion, we explore the application of Gauss's Law to determine the electric field inside a spherical conductor with a negative charge, denoted as -Q. A fundamental property of conductors is that any net charges will redistribute themselves along the surface to maximize their distance from one another. This means that for a conductor with a net charge of -Q, all negative charges will be evenly distributed on the surface.

To analyze the electric field within the conductor, we need to select an appropriate Gaussian surface. Given the spherical symmetry of the conductor, a spherical Gaussian surface is the most suitable choice. The goal is to find the electric field inside the conductor, so we position our Gaussian surface within the conductor itself.

According to Gauss's Law, the total electric flux through the Gaussian surface is given by the equation:

$$\Phi_E = E \cdot A = \frac{Q_{\text{enc}}}{\varepsilon_0}$$

where \(E\) is the electric field, \(A\) is the area of the Gaussian surface, \(Q_{\text{enc}}\) is the enclosed charge, and \(\varepsilon_0\) is the permittivity of free space.

In this scenario, since the Gaussian surface is located inside the conductor, the enclosed charge \(Q_{\text{enc}}\) is zero. This is because all the charges reside on the surface of the conductor, leaving no charge within the interior. Consequently, we can simplify the equation:

$$E \cdot A = \frac{0}{\varepsilon_0}$$

Since the area \(A\) is not zero, it follows that the electric field \(E\) must also be zero:

$$E = 0$$

This conclusion aligns with the established principle that the electric field inside a conductor in electrostatic equilibrium is always zero. Thus, Gauss's Law effectively reinforces this concept, demonstrating that in the absence of enclosed charge within the Gaussian surface, the electric field must be zero. This understanding is crucial for grasping the behavior of electric fields in conductive materials.

Rank the flux through surfaces A, B and C in the figure below from greatest to smallest.

• A. Φ_C, Φ_B, Φ_A
• B. Φ_A, Φ_B, Φ_C
• C. Φ_A, Φ_C, Φ_B
• D. Φ_B, Φ_C, Φ_A

Answer: (D)

Electric Field due to Hollow Shell

Understanding the electric field around a conducting spherical shell is crucial in electrostatics, particularly when applying Gauss's Law. This law states that the electric flux through a closed surface is proportional to the charge enclosed by that surface. To analyze the electric field in three distinct regions—inside the shell but outside a point charge, within the conducting shell, and outside the shell—we can utilize Gaussian surfaces.

For the first region, where we are outside the point charge but inside the conducting shell, we can draw a Gaussian surface in the shape of a sphere. The electric field lines radiate outward from the point charge, and since the normals to the surface also point outward, the angle between them is zero. Thus, the cosine of the angle is one, simplifying our calculations. The electric flux, given by the equation:

$$\Phi_E = E \cdot A = E \cdot 4\pi r^2$$

is equal to the enclosed charge divided by the permittivity of free space, represented as:

$$\Phi_E = \frac{Q_{enc}}{\epsilon_0}$$

By equating these two expressions, we find that the electric field \(E\) due to a point charge \(Q\) at a distance \(r\) is:

$$E = \frac{1}{4\pi \epsilon_0} \cdot \frac{Q}{r^2}$$

This formula indicates that the electric field behaves like that of a point charge, diminishing with the square of the distance from the charge.

In the second region, which is within the conducting shell, we again use a spherical Gaussian surface. A key principle to remember is that the electric field inside a conductor in electrostatic equilibrium is always zero. This occurs because any charge within the conductor redistributes itself to cancel out any internal electric fields. Although there is a positive charge \(Q\) at the center, the conductor's inner surface acquires a charge of \(-Q\), leading to a net enclosed charge of zero. Therefore, the electric field \(E\) inside the conducting shell is:

$$E = 0$$

Finally, in the third region, which is outside the conducting shell, we again draw a Gaussian surface. The total charge enclosed by this surface includes the positive charge \(Q\) at the center and the induced charge on the outer surface of the conductor, which is also \(+Q\). Thus, the total enclosed charge remains \(Q\). The electric field can be calculated similarly to the first region, yielding:

$$E = \frac{1}{4\pi \epsilon_0} \cdot \frac{Q}{r^2}$$

This result shows that outside the conducting shell, the electric field behaves as if all the charge were concentrated at a point at the center of the shell, reaffirming the concept that the electric field outside a spherical conductor is equivalent to that of a point charge.

In summary, the electric field behaves distinctly in each of the three regions surrounding a conducting spherical shell, demonstrating the principles of Gauss's Law and the behavior of electric fields in conductors.

Surface Charge Density

In this example, we explore the concept of surface charge density on the inner and outer surfaces of a conductor. Understanding the distribution of electric charge is crucial, particularly in the context of Gauss's Law, which states that the electric field inside a conductor is zero when in electrostatic equilibrium. This means that any charge present will reside on the surfaces of the conductor.

For a conductor with a total charge of -3 coulombs on the inner surface, the outer surface will have a charge of +3 coulombs due to charge conservation. The surface charge density, denoted by the symbol σ, is defined as the total charge Q divided by the total area A of the surface:

σ = \frac{Q}{A}

It is important to note that the charge Q used here is not the enclosed charge typically referenced in Gaussian surfaces, but rather the charge distributed on the surface of the conductor.

To calculate the surface charge density on the inner wall, we first determine the area of the inner surface. For a spherical conductor, the area is given by:

A = 4\pi r^2

Given that the inner radius is 3 cm (or 0.03 m), the area becomes:

A_{inner} = 4\pi (0.03)^2 = 1.13 \times 10^{-2} \, m^2

Substituting the values into the surface charge density formula for the inner wall:

σ_{inner} = \frac{-3 \, C}{1.13 \times 10^{-2} \, m^2} \approx -265 \, C/m^2

Next, we calculate the surface charge density on the outer wall. The outer radius is 5 cm (or 0.05 m), leading to an area of:

A_{outer} = 4\pi (0.05)^2 = 3.14 \times 10^{-2} \, m^2

Using the charge on the outer surface, we find:

σ_{outer} = \frac{3 \, C}{3.14 \times 10^{-2} \, m^2} \approx 95 \, C/m^2

This analysis reveals that the surface charge density on the inner surface is negative, while that on the outer surface is positive, reflecting the nature of the charges distributed across the respective areas. Understanding these principles is essential for grasping electrostatics and the behavior of conductors in electric fields.

A spherical, thin conducting shell of radius 8cm has a charge of –6C. If a 4C charge were placed at the center of the shell, what is the electric field 4 cm from the center? At 12 cm?

• A. E_4cm = 2.25 × 10⁹ outwards;E_12cm = 1.25 × 10⁸ inwards
• B. E_4cm = 2.25 × 10¹³ outwards;E_12cm = 1.25 × 10¹³ outwards
• C. E_4cm = 2.25 × 10¹³ outwards;E_12cm = 6.25 × 10¹² outwards
• D. E_4cm = 2.25 × 10¹³ outwards;E_12cm = 1.25 × 10¹² inwards

Answer: (D)

Here’s what students ask on this topic:

What is Gauss's Law and how is it used in electrostatics?

Gauss's Law states that the net electric flux through a closed surface is proportional to the charge enclosed within that surface. The mathematical expression is:

$\Phi$_net = Qε₀

where $\Phi$_net is the net flux, $Q$ is the enclosed charge, and $\epsilon$₀ is the permittivity of free space. This law simplifies the calculation of electric fields and flux, especially for symmetric charge distributions. By choosing an appropriate Gaussian surface, one can easily relate the enclosed charge to the electric field, making it a powerful tool in electrostatics.

How do you calculate electric flux using Gauss's Law?

To calculate electric flux using Gauss's Law, follow these steps:

1. Identify the closed surface (Gaussian surface) that encloses the charge.
2. Determine the total charge $Q$ enclosed within the surface.
3. Use the formula:

$\Phi$_net = Qε₀

4. Substitute the values of $Q$ and $\epsilon$₀ (8.85 × 10^-12 C²/N·m²) into the equation.
5. Calculate the net flux $\Phi$_net.

This method allows you to find the electric flux through a closed surface without needing to integrate the electric field over the surface.

What are the common types of problems solved using Gauss's Law?

There are three common types of problems solved using Gauss's Law:

1. Calculating Flux from Charge: Given a charge distribution, determine the net electric flux through a closed surface using $\Phi$_net = Qε₀.
2. Calculating Charge from Flux: Given the net electric flux through a closed surface, determine the enclosed charge using $Q=\Phi$_netε₀.
3. Deriving Electric Field: Use Gauss's Law to derive the electric field for symmetric charge distributions (e.g., point charges, spherical, cylindrical, or planar symmetry) by choosing an appropriate Gaussian surface.

These problems highlight the versatility and power of Gauss's Law in simplifying complex electrostatic calculations.

How do you choose a Gaussian surface for solving problems using Gauss's Law?

Choosing a Gaussian surface involves selecting a surface that exploits the symmetry of the charge distribution to simplify calculations. The three main types of Gaussian surfaces are:

1. Spheres: Used for point charges or spherically symmetric charge distributions. The electric field is constant at a given radius.
2. Cylinders: Used for line charges or cylindrically symmetric charge distributions. The electric field is constant at a given radial distance from the axis.
3. Planes: Used for infinite plane charges or planar symmetry. The electric field is constant at a given distance from the plane.

By choosing a surface where the electric field is constant and the angle between the field and the surface normal is zero, you can simplify the flux calculation to $\Phi =EA$.

What is the significance of the permittivity of free space (ε₀) in Gauss's Law?

The permittivity of free space, denoted as $\epsilon$₀, is a fundamental physical constant that characterizes the ability of the vacuum to permit electric field lines. Its value is approximately 8.85 × 10^-12 C²/N·m². In Gauss's Law, it appears in the denominator of the equation:

$\Phi$_net = Qε₀

This constant ensures that the relationship between electric flux and enclosed charge is correctly scaled. It plays a crucial role in determining the strength of the electric field generated by a given charge distribution in a vacuum.