Electric Flux: Study with Video Lessons, Practice Problems & Examples

Electric flux measures how much electric field passes through a surface, akin to water flowing through a ring. It depends on the angle between the electric field and the surface's normal vector. The equation for electric flux is Φ = EAcosθ. Positive flux occurs when the electric field and normal point in the same direction, while negative flux occurs when they point in opposite directions. The total flux through a closed surface is the sum of individual fluxes across its surfaces.

Electric Flux

Hey guys. So for this video, I want to talk about electric flux. It's a concept that is very important in electrostatics. You'll definitely need it to solve problems, especially when we start talking about Gauss's law. So let's go ahead and check it out. Basically, the flux of anything is just a measure of how much of something passes through a surface. The way I like to think about this is kind of like if this field here was like a river and you were to stick like a ring inside of it, how much water passes through the ring? That's sort of how I like to think about flux. So when we talk about electric flux, we're going to be talking about the electric field and specifically how much of this electric field will pass through a surface. OK. So we've got these couple of examples right here, imagine these blue lines represent the electric field and this represents just a surface kind of like a ring I was just talking about. Well, in this situation, basically the flux is how much of these lines will pass through the surface. And in this case, we can say that this ring has sort of caught all of these electric field lines. So that means the electric flux is going to be all or maximum or something like that. Whereas in this situation, now we're going to have the ring, but instead of it being upright and all the field lines passing through it, what happens is that these electric field lines will pass directly over it. So imagine you were to turn that ring and instead of it being upright, you were to turn it on its side, no field lines would actually go through that ring that would kind of just go right over it or underneath it. So that means that the electric flux at this point is none or is nothing, there is no electric flux because there's nothing actually passing through the surface. Remember that the electric field that passes through the surface is defined as the electric flux. And then in this situation, we have somewhere in the middle. So some of the field lines are actually passing over it and under it. And then some of them are passing through. But at some angle here. And so in this case, the electric field line isn't an all or nothing, it's actually just some. So it's some partial amount of electric flux. So clearly what we've seen in these three examples is that the electric flux depends on the angle of the surface. Now, the way we measure this angle is we say the electric field lines make some angle with something called the normal of the surface. And the way I like to think about the normal is if my hand, the back of my hand was a surface, then there is a vector that points directly perpendicular to that surface, that's called the normal. And since the normal is the perpendicular of that surface, then the electric flux is going to be dependent on the angle that the electric field makes with that surface. And this angle here is measured between the electric fields which are the blue lines and the normal or the perpendicular vector of that surface. And if you have all those three things together, then the electric flux has an equation. It's going to be EAcosθ . Now there are some units associated with electric flux, you might not need to know them, but you can always get them back from the electric fields and the areas and things like that. And so if you have a bunch of surfaces together, not just one of them, you can calculate something called the total amount of flux, which is what we're going to use later on in the chapter. So the total amount of flux through a closed surface is just going to be the sum of all the fluxes through the individual surfaces. Now, I want to be very, very careful here about how I explain this but a closed surface, you guys might be wondering what that is, a closed surface is just sort of any boundary that encloses some volume. So the easiest one to think of is like a box. So imagine like this, right? So I have a box and yep. So that means that if there were some electric field lines sort of passing through this box, well, this box has six individual surfaces, right? So you have a flux that's going here, flux is going here, here on the bottom, on the front. And then also, I think I'm missing one somewhere over here, right? So you have these individual fluxes from these individual surfaces, but the closed surface represents sort of like that three-dimensional object that I've made here. And so the total flux to calculate through this closed surface is just going to be the sum of all the fluxes through the individual surface. And when we're doing that and we're calculating total fluxes, we know that we can have sometimes you can end up with positives and negative fluxes. Now, usually in physics, positives and negatives have to do with direction. So let's go ahead and check out the two different cases, you're going to get a positive flux whenever the electric field and the normal point in the same direction. Now why? Because if you take a look at this equation right here, if we say that these electric field lines are E and this normal or this normal, which we usually represent by the area vector point in the same direction, then we know that the cosine of the angle is going to be zero. And what's the cosine of zero, it's just positive one. So that means it's just going to correspond to a positive flux. Whereas you're going to get the opposite and negative flux whenever the electric field and the normal point in opposite directions. Now, you can probably guess why because in this case, the cosine of the angle is 180 degrees, and cosine of 180 is negative one. So the way I like to think about this is if the electric field lines are going out of a surface, it's going to be positive. But if the electric field lines are going inside of a surface, then it's going to be negative, right? That's basically the last thing I want you to know about electric fluxes. Let's go ahead and take a look at a quick example. So you've got the electric flux through each surface of a cube. So kind of like the example that I showed you above is given below. So what's the total flux through the cube? All we have to do is if you have the, if you have φ_1 + φ_2 + φ_3 + φ_4 + φ_5 + φ_6, then the net is just going to be the addition of all of them. So φ_1 + φ_2 + φ_3 + φ_4 + φ_5 + φ_6. By the way, these Greek letters right here are the letter phi. So sometimes I'll say that. So basically all you have to do is just add all of these things up. The zeros don't contribute anything. So you just have to do 100 plus 20 minus 40 minus 80 just go ahead and add all that stuff up. Well, 100 plus 20 is 120 and then negative 40 negative 80 is negative 120. So that means that the net electric flux here, φ_{net} = 0, right? And that's it. So that's basically how you would add up together these electric fluxes. Let's go ahead and take it a bunch more examples in the next coming videos. All right, let me know if you have any questions.

The electric flux through each surface of a cube is given below. Which surfaces of the cube does the electric field run parallel to? 

Φ₁ = 100 Nm² /C      Φ₄ = 0 Nm² /C

Φ₂ = 20 Nm² /C       Φ₅ = −40 Nm² /C

Φ₃ = 0 Nm² /C        Φ₆ = −80 Nm² /C

• A. 1 and 2
• B. 3 and 4
• C. 5 and 6
• D. 1, 2, 5, and 6

Flux Through Angled Surface

Alright, guys, let's get some more practice with this electric flux stuff. So, we have this electric field, and we have the area of the surface, and we're told to find what the magnitude of the electric flux is through the surface depicted. So let's go ahead and start with the equation. The electric flux is just going to be the magnitude of the electric field times the area times the cosine of the angle theta.

Now, if you take a look at this, we actually know what the electric field is. We have that, and we're told the area of the surface is just 1 m² and it's in the right units. So the only thing we have to find is what the cosine of the angle is. And what I want you guys to do is remember that when we're dealing with cosines of angles, especially with this electric flux, this angle represents the angle between the area or the normal of the surface and the electric field. So if we sort of extend these electric field lines out like this, then what we really need to do is find what the normal of the surface is. The normal of the surface is always perpendicular to the surface itself. So it points out in that direction.

And the reason we're told to find the magnitude of the electric flux is because we actually have no idea, we have no information on whether the normal is pointing this way or this way. So we're just going to go ahead and assume that it's positive by calculating the magnitude of the electric flux anyway. So the angle that we really need is actually the angle between this vector and the normal of the surface, which is not the same as this 30 degrees. This 30 degrees is the angle between the electric field and the surface itself, not the perpendicular of that surface.

So really, we're not using this 30 degrees. Instead, we're just going to use 30 plus 60 equals 90, so this angle is actually 60 degrees, which is this angle as well by the geometry; these things are all opposite angles. So what we really need to do is compute the electric flux, which is going to be:

Φ = 100 Newtons per Coulomb × 1 m 2 × cos ( 60 ° )

Now, cos(60) is just one half. So that means the electric flux is just half of 100, which is 50. And that electric flux is in units of Newton meters squared per coulomb. Alright, so that's the answer. Let me know if you guys have any questions.

Flux Through Cube

Alright, guys, let's work this one out together. So we have a cube and its side length is two centimeters and it's placed in a uniform electric field. We've got two centimeters right here. We're supposed to figure out what the electric flux is through each side of the cube. So let's go ahead and visualize what's going on here. First, we're going to draw the normal vectors for each one of those sides. So the top one has a normal vector like this. This one has one that goes sort of like outwards like this. Think one has one to the right, one's got one to the left, and then there is a bottom one that's going to point downward. And there's going to be a back one sort of on the backside of the cube. Anyway, each one of these surfaces now may or may not have an electric field that goes through it, so we know we're going to have to calculate the electric flux for all of these. So just remember that it's EAcosθ for the electric flux.

Clearly, we can see that for the right side, there is definitely going to be some electric flux here. So the right side is just going to be EAcosθ. But in this case, we have the EA. The cosine of the angle is just going to be zero. So this is just going to be EA. Whereas on the other side, we could make the opposite argument that you have the same exact area because it's a cube. Except in this case, the flux on the left side is just going to be EAcosπ. So it's going to be equal to negative EA.

Now, let's see what's going on for the top side. You have an electric field that points in one direction, and you have a normal vector that points upward. That means that the cosine of this angle right here that it makes is equal to zero. So that means that over here the flux at the top is just equal to zero. By the same reasoning, the flux at the bottom is also equal to zero.

Now, the only two remaining are the front and the back side. So now you have an electric field that points in one direction, and now you have a normal that points straight out, as if I was pointing directly at you. So this angle is also still 90 degrees, even though it's just a different orientation due to our three-dimensional coordinate system. So that means the flux on the front, which, by the way, is going to be equal to the flux on the backside because this is symmetrical, is also going to be equal to zero.

So in other words, we have found that the front, the back, the bottom, and the top are all equal to zero, and the only two surfaces that actually have non-zero flux going through them are going to be the left and the right side. So let's see, we've got 100 Newtons per Coulomb and now we have a side length of two centimeters. So the area over here is equal to two centimeters times two centimeters. That's going to be four square centimeters. But you have to be careful because any time you want to convert this to meters, you have to actually adjust the decimal place two times because you have to do this conversion four times. So this is actually going to be 0.0004 metres squared.

The electric flux is going to be negative 0.04 on the left side and a positive 0.04 on the right side, as if it's just going to be the positive of the negative value on the left side. Those are the fluxes for each one of these sides. Let me know if you guys have any questions.

Where does the normal vector point for a spherical shell?

• A. Radially inward
• B. Radially outward
• C. Perpendicular to the radius
• D. A normal vector does not exist

Flux Through Spherical Shell due to Point Charge

Hey, guys. So for this example, we're going to build off of something that we talked about in the last example. We were asked to find out what the electric flux is through a spherical shell of radius r due to some point charge that's in the center. So we're asked for the electric flux. Let's go ahead and start with our electric flux formula. We've got E times A times the cosine of θ, in which this θ is between the normal vector and the electric field at that specific point. So the first thing is, first, where's the electric field? Points due to a point charge? Well, at any surface here, it always points away from that point charge. Remember, the electric field lines always point outwards, but at the same time, the normal vector of a spherical shell also always points outward directly at the surface. So these perpendicular lines here, the normals, are always going to point away from that spherical shell, which means that the cosine of the angle right here, this θ, wherever you look along the surface, these field lines and the normal always point in the same exact direction. Since the θ is always equal to zero, that means this cosine of θ is always just going to be equal to one, no matter where you are that you're looking at. So that means that the total amount of electric flux is going to be the total amount of electric field times the total amount of area.

So the electric field, let's see, the electric field due to a point charge is kQ/R2. So at some distance R, that's going to be R2. So that's the electric field due to this point charge and the area of the spherical shell, the surface area of a sphere, is just 4πR2. So if you go ahead and put those two things together, that means that the electric flux is going to be kQ/R2×4πR2. Now what happens is the R2 will cancel. And so we end up just getting that the flux is equal to 4πkQ.

This is the answer for 4πkQ. There's actually another way that we could write this because we know that this k has a relationship with that ε₀, the permittivity constant. Remember that this k is equal to 14πε₀. The reason we want to make this substitution is that now the 4π will cancel, so this actually will turn into Q/ε₀. This is a really important result. We're going to talk about it much later when we get to Gauss's law. That's just another way you could express this, by the way. So, both of these things would actually be perfectly valid if you were given this on a test or anything like that.

All right, This is the answer, or this is the answer. Let me know if you guys have any questions.

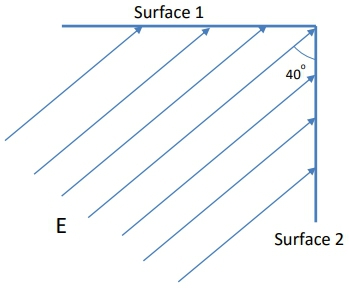
What is the total flux through the two surfaces depicted in the following figure? Note that surface 1 has an area of 50 cm² and surface 2 has an area of 100 cm² , and E = 500 N/C.

• A. 513 N•m²/C
• B. 3.74 N•m²/C
• C. 3.16 N•m²/C
• D. 5.13 N•m²/C
• E. 5.44 N•m²/C

Here’s what students ask on this topic:

What is electric flux and how is it calculated?

Electric flux is a measure of how much electric field passes through a given surface. It is analogous to the amount of water flowing through a ring. The electric flux (Φ) depends on the electric field (E), the area of the surface (A), and the angle (θ) between the electric field and the normal to the surface. The formula for electric flux is:

$\Phi =EAcos\left(\theta \right)$

What is the significance of the angle in the electric flux equation?

The angle (θ) in the electric flux equation is the angle between the electric field (E) and the normal (perpendicular vector) to the surface. This angle determines how much of the electric field passes through the surface. When θ is 0 degrees, the electric field is perpendicular to the surface, and the flux is maximized. When θ is 90 degrees, the electric field is parallel to the surface, and the flux is zero. The flux is calculated using the cosine of this angle:

$\Phi =EAcos\left(\theta \right)$

How do you calculate the total electric flux through a closed surface?

The total electric flux through a closed surface is the sum of the electric fluxes through each individual surface that makes up the closed surface. For example, if you have a box with six surfaces, you calculate the flux through each surface and then sum them up. The formula is:

$\Phi {\mathrm{total}}_{}=\sum _{}^{i=1}{\Phi }_i$

Positive flux occurs when the electric field and the normal point in the same direction, while negative flux occurs when they point in opposite directions.

What are the units of electric flux?

The units of electric flux are derived from the units of the electric field (E) and the area (A). The electric field is measured in newtons per coulomb (N/C) or volts per meter (V/m), and the area is measured in square meters (m²). Therefore, the units of electric flux are:

$\Phi =EA=\frac{N}{C}·m^2$

What is the difference between positive and negative electric flux?

Positive electric flux occurs when the electric field (E) and the normal to the surface point in the same direction. This is because the cosine of the angle (θ) between them is positive. Negative electric flux occurs when the electric field and the normal point in opposite directions, resulting in a negative cosine value. In simpler terms, if the electric field lines are exiting a surface, the flux is positive; if they are entering a surface, the flux is negative.