Electric Fields in Capacitors: Videos & Practice Problems

Capacitors consist of two parallel plates with equal and opposite charges, creating a uniform electric field directed from the positive to the negative plate. The electric field (E) can be calculated using the equation $Q/\epsilon A$, where Q is the charge, ε is the vacuum permittivity (approximately 8.85 x 10^-12 F/m), and A is the area of the plates. Understanding capacitors is essential for grasping how they store charge and energy in electrical circuits.

Intro to Capacitors

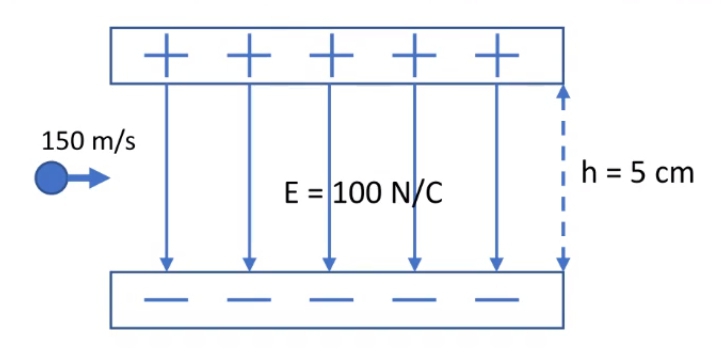
Capacitors are essential components in electrical circuits, consisting of two parallel plates that hold equal and opposite charges, creating a uniform electric field between them. This electric field, denoted as E, is directed from the positive plate to the negative plate and remains constant at all points within the space between the plates. The uniformity of the electric field arises because the electric fields produced by the charges on the plates cancel each other out symmetrically, resulting in a consistent direction and magnitude.

The relationship between the electric field and the charge on the plates can be expressed with the equation:

\( E = \frac{Q}{\varepsilon_0 A} \)

In this equation, Q represents the charge on each plate, A is the area of the plates, and \(\varepsilon_0\) is the vacuum permittivity, a constant valued at approximately \( 8.85 \times 10^{-12} \, \text{F/m} \). This constant is related to Coulomb's constant, \( K \), through the equation:

\( K = \frac{1}{4 \pi \varepsilon_0} \)

For practical calculations, if the electric field between the plates is known, along with the area of the plates, one can rearrange the equation to solve for the charge:

\( Q = \varepsilon_0 A E \)

When working with the area of the plates, it is crucial to convert units correctly. For example, if the area is given in square centimeters, it must be converted to square meters by applying the conversion factor twice (since area is a two-dimensional measurement). For instance, \( 5 \, \text{cm}^2 \) converts to \( 5 \times 10^{-4} \, \text{m}^2 \).

In summary, capacitors store electrical energy by maintaining a charge difference between their plates, and the electric field generated between them is a fundamental concept in understanding their behavior in circuits. The ability to calculate the charge based on the electric field and plate area is a key skill in electrical engineering and physics.

Example 1

In this discussion, we explore the relationship between charge, area, and the electric field produced by a capacitor. The electric field (E) between two parallel plates is defined by the equation:

E = \(\frac{Q}{\epsilon_0 A}\)

where Q is the charge on one plate, \(\epsilon_0\) is the permittivity of free space, and A is the area of the plates. To analyze the effect of changing these variables, we consider a scenario where the charge is doubled and the area is halved.

Let’s denote the new charge as Q_new = 2Q and the new area as A_new = \frac{1}{2}A. Substituting these values into the electric field equation gives:

E_new = \(\frac{Q_{new}}{\epsilon_0 A_{new}} = \frac{2Q}{\epsilon_0 \left(\frac{1}{2}A\right)}\)

By simplifying this expression, we can factor out the constants:

E_new = \(\frac{2Q}{\epsilon_0} \cdot \frac{2}{A} = \frac{4Q}{\epsilon_0 A}\)

Notice that \(\frac{Q}{\epsilon_0 A}\) is the original electric field (E). Therefore, we can express the new electric field as:

E_new = 4E

This indicates that when the charge is doubled and the area is halved, the new electric field becomes four times stronger than the original electric field. This relationship highlights the direct proportionality of the electric field to the charge and its inverse relationship to the area of the plates.

An electron moves into a capacitor at an initial speed of 150 m/s. If the electron enters exactly halfway between the plates, how far will the electron move horizontally before it strikes one of the plates? Which plate will it strike?

• A. 8.0×10⁻⁶ m
• B. 8.0×10⁻⁵ m
• C. 1.1×10⁻⁵ m
• D. 1.1×10⁻⁴ m

Answer: (A)

Here’s what students ask on this topic:

What is the electric field between the plates of a capacitor?

The electric field (E) between the plates of a capacitor is uniform and directed from the positive plate to the negative plate. It can be calculated using the equation:

$E=\frac{Q}{\epsilon A}$

where $Q$ is the charge on each plate, $\epsilon$ is the vacuum permittivity (approximately 8.85 x 10^-12 F/m), and $A$ is the area of the plates. This uniform field is the same at all points between the plates.

How do capacitors store energy?

Capacitors store energy in the electric field created between their plates. When a voltage is applied across the plates, charges accumulate on them, creating an electric field. The energy (U) stored in a capacitor can be calculated using the equation:

$U=\frac{1}{2}C{V}^2$

where $C$ is the capacitance of the capacitor and $V$ is the voltage across the plates. This energy is stored in the electric field and can be released when the capacitor is discharged.

What is the role of vacuum permittivity in capacitors?

Vacuum permittivity, denoted as $\epsilon$₀, is a constant that describes how electric fields interact with the vacuum. Its value is approximately 8.85 x 10^-12 F/m. In capacitors, vacuum permittivity is used in the equation for the electric field between the plates:

$E=\frac{Q}{\epsilon A}$

where $Q$ is the charge on each plate and $A$ is the area of the plates. It also relates to Coulomb's constant (k) through the equation:

$k=\frac{1}{4\pi \epsilon }$₀

How do you calculate the charge on each plate of a capacitor?

To calculate the charge (Q) on each plate of a capacitor, you can use the equation for the electric field (E) between the plates:

$E=\frac{Q}{\epsilon A}$

Rearranging this equation to solve for Q gives:

$Q=E\epsilon A$

where $E$ is the electric field, $\epsilon$ is the vacuum permittivity (approximately 8.85 x 10^-12 F/m), and $A$ is the area of the plates. By plugging in the values for E, $\epsilon$, and A, you can determine the charge on each plate.

What happens to the electric field outside the plates of a capacitor?

Outside the plates of a capacitor, the electric field is essentially zero. This is because the fields produced by the positive and negative charges on the plates cancel each other out. Inside the plates, the electric field is uniform and directed from the positive to the negative plate, but outside, the fields from each plate oppose each other, resulting in no net electric field. This is a key characteristic of the parallel plate capacitor configuration.