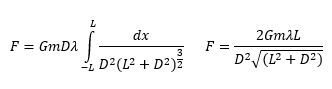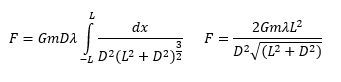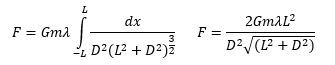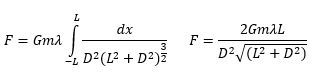Mass Distribution with Calculus: Videos & Practice Problems

Calculus is essential for calculating gravitational forces in non-spherical mass distributions. Using Newton's law of gravitation, we treat differential mass elements (dm) as point masses, generating tiny forces (dF) that we integrate to find total force (F). The equation is expressed as F^2 = GM⁢r^2 + d^2. This approach allows for accurate calculations in gravitational problems involving complex shapes.

Using Calculus to Solve Mass Distribution Problems

In the study of gravitational forces, particularly for non-spherical mass distributions, we utilize calculus to derive the gravitational force acting on a mass due to a distribution of mass. According to Newton's law of gravity, the gravitational force \( F \) between two point masses \( m_1 \) and \( m_2 \) separated by a distance \( r \) is given by the equation:

\( F = \frac{G m_1 m_2}{r^2} \)

For spherical objects, we can simplify the problem by treating the mass as concentrated at a point, specifically at the center of mass. However, when dealing with non-spherical distributions, this simplification is no longer valid. Instead, we can break the mass into infinitesimally small pieces, referred to as differential mass elements \( dm \). Each of these elements can be treated as a point mass, generating a tiny gravitational force \( dF \) on another mass \( m \) located at a distance \( r \) from the mass element.

The expression for the differential force \( dF \) due to a differential mass \( dm \) is given by:

\( dF = \frac{G \, dm \, m}{r^2} \)

To find the total gravitational force \( F \), we need to integrate \( dF \) over the entire mass distribution:

\( F = \int dF = G m \int \frac{dm}{r^2} \)

In this integral, \( G \) and \( m \) can be factored out as constants since they do not change during the integration process. The next step involves determining the expression for \( r \) based on the geometry of the mass distribution. For example, if we consider a hollow ring, we can use the Pythagorean theorem to express \( r \) as:

\( r = \sqrt{R^2 + d^2} \)

where \( R \) is the radius of the ring and \( d \) is the distance from the center of the ring to the mass \( m \).

Next, we decompose the total force into its x and y components. Due to symmetry, the y-components of the forces from opposite sides of the ring will cancel each other out, leaving only the x-components contributing to the total force. The x-component of the differential force can be expressed as:

\( dF_x = dF \cos(\theta) \)

Using the relationship of the triangle formed by the geometry, we can express \( \cos(\theta) \) in terms of the sides of the triangle, leading to:

\( dF_x = \frac{G m}{r^2} \cdot \frac{d}{r} \)

Substituting the expression for \( r \) into the equation, we can simplify the integral further. After pulling out constants from the integral, we arrive at:

\( F = \frac{G M d}{(R^2 + d^2)^{3/2}} \int dm \)

Since the integral of \( dm \) over the entire mass distribution equals the total mass \( M \), we finally obtain the expression for the gravitational force:

\( F = \frac{G M^2 d}{(R^2 + d^2)^{3/2}} \)

This formula allows us to calculate the gravitational force exerted by a non-spherical mass distribution, such as a hollow ring, on a point mass located at a distance \( d \) from the center of the ring.

Gravitational Force of Rod Parallel to Axis

To determine the gravitational force between a rod of mass \( m \) and length \( l \) and another mass, we start by using the gravitational force formula, which is expressed as:

\[ F = G \cdot M \cdot \int \frac{dm}{r^2} \]

Here, \( G \) is the gravitational constant, \( M \) is the mass of the other object, and \( r \) is the distance between the mass elements of the rod and the other mass. Since the rod is a mass distribution rather than a point mass, we need to set up an integral to account for the varying distances.

Next, we define the distance \( r \) in terms of the length of the rod and a variable \( x \), which represents a position along the rod. The relationship can be expressed as:

\[ r = l + d - x \]

where \( d \) is the distance from the end of the rod to the mass. This expression shows that \( r \) changes depending on the position \( x \) along the rod.

Since the gravitational force acts along the x-axis, we can simplify our calculations by noting that the force does not have components in the y-direction. Thus, we can directly use the integral without breaking it into components.

Substituting our expression for \( r \) into the integral, we have:

\[ F = G \cdot M \cdot \int \frac{dm}{(l + d - x)^2} \]

To relate the mass element \( dm \) to the length of the rod, we use the linear mass density \( \lambda \), defined as:

\[ \lambda = \frac{m}{l} \]

Thus, we can express \( dm \) as:

\[ dm = \lambda \cdot dx = \frac{m}{l} \cdot dx \]

Substituting this into our force equation gives:

\[ F = G \cdot M \cdot \int_0^l \frac{\frac{m}{l} \, dx}{(l + d - x)^2} \]

Now, we can pull out the constants from the integral:

\[ F = \frac{G \cdot M \cdot m}{l} \cdot \int_0^l \frac{dx}{(l + d - x)^2} \]

Next, we need to evaluate the integral. To do this, we can use a substitution method. Let:

\[ u = l + d - x \]

Then, the differential \( dx \) becomes:

\[ dx = -du \]

Changing the limits of integration accordingly, when \( x = 0 \), \( u = l + d \), and when \( x = l \), \( u = d \). Thus, the integral transforms to:

\[ F = \frac{G \cdot M \cdot m}{l} \cdot \int_{l + d}^{d} \frac{-du}{u^2} \]

This integral can be simplified to:

\[ F = \frac{G \cdot M \cdot m}{l} \cdot \left[ \frac{1}{u} \right]_{l + d}^{d} \]

Evaluating this gives:

\[ F = \frac{G \cdot M \cdot m}{l} \cdot \left( \frac{1}{d} - \frac{1}{l + d} \right) \]

Thus, the final expression for the gravitational force between the rod and the mass is:

\[ F = \frac{G \cdot M \cdot m}{l} \left( \frac{1}{d} - \frac{1}{l + d} \right) \]

This result encapsulates the gravitational interaction between a mass distribution and a point mass, highlighting the importance of integrating over the mass distribution to accurately calculate the force.

a) Set up the integral for the gravitational force between a rod with a density λ and length 2L, and a mass m at an arbitrary distance D directly above the midpoint of the rod.
b) Evaluate the integral.

• A.
• B.
• C.
• D.

Answer: (A)

Gravitational Force from a Solid Disk

In this example, we explore the calculation of the gravitational force between a solid disk and a small mass located outside the disk. To simplify the problem, we conceptualize the disk as composed of thin concentric rings, allowing us to apply techniques used in previous ring problems.

The gravitational force \( F \) can be expressed using the formula:

\( F = G \cdot m \cdot \int \frac{dm}{r^2} \)

where \( G \) is the gravitational constant, \( m \) is the mass of the small object, and \( dm \) is the mass element of the disk. The distance \( r \) from the mass element to the small mass is derived from the geometry of the disk, specifically using the relationship:

\( r = \sqrt{r'^{2} + d^{2}} \)

Here, \( r' \) is the radius of the thin ring, and \( d \) is the distance from the disk to the mass.

Next, we break down the gravitational force into its x and y components. Due to symmetry, the y-components of the forces from opposite rings cancel each other out, leaving only the x-components to contribute to the total force. The x-component can be expressed as:

\( dF_x = dF \cdot \cos(\theta) \)

where \( \cos(\theta) \) is determined from the triangle formed by the disk and the mass, leading to:

\( \cos(\theta) = \frac{d}{r} \)

Substituting this into our force equation gives:

\( F = G \cdot m \cdot \int \frac{dm \cdot d}{r^3} \)

We then replace \( r \) with its expression in terms of \( r' \) and \( d \):

\( F = G \cdot m \cdot d \cdot \int \frac{dm}{(r'^{2} + d^{2})^{3/2}} \)

To relate \( dm \) to the area of the disk, we use the total mass \( M \) and total area \( A \) of the disk, where:

\( A = \pi R^{2} \)

Thus, the differential area \( dA \) for a thin ring is given by:

\( dA = 2\pi r' \, dr' \)

Consequently, we can express \( dm \) as:

\( dm = \frac{M}{A} \cdot dA = \frac{M}{\pi R^{2}} \cdot 2\pi r' \, dr' = \frac{2M}{R^{2}} r' \, dr' \)

Substituting this back into our force equation results in:

\( F = \frac{G \cdot m \cdot M \cdot d}{R^{2}} \cdot \int_{0}^{R} \frac{2r' \, dr'}{(r'^{2} + d^{2})^{3/2}} \)

To evaluate the integral, we perform a substitution where \( u = r'^{2} + d^{2} \), leading to:

\( du = 2r' \, dr' \)

Thus, the integral simplifies, and we can evaluate it at the limits \( r' = 0 \) to \( r' = R \). The final expression for the gravitational force becomes:

\( F = \frac{2G \cdot m \cdot M}{R^{2}} \left( \frac{1}{d} - \frac{1}{\sqrt{R^{2} + d^{2}}} \right) \)

This formula provides the gravitational force exerted by the disk on the small mass located outside of it, taking into account the contributions from all the infinitesimal mass elements of the disk.

Here’s what students ask on this topic:

How do you calculate the gravitational force for non-spherical mass distributions using calculus?

To calculate the gravitational force for non-spherical mass distributions using calculus, we break the mass into tiny differential elements (dm) and treat each as a point mass. Each differential mass generates a tiny force (dF) that we integrate to find the total force (F). The equation is expressed as:

$F^2=GM{r}^2+d^2$

This approach allows for accurate calculations in gravitational problems involving complex shapes.

What is the role of differential mass (dm) in calculating gravitational forces?

Differential mass (dm) plays a crucial role in calculating gravitational forces for non-spherical mass distributions. By breaking the mass into tiny differential elements (dm), we can treat each element as a point mass. Each differential mass generates a tiny force (dF), which we then integrate to find the total gravitational force (F). This method allows us to account for the varying distribution of mass and accurately calculate the gravitational force.

Why can't we use Newton's law of gravity directly for non-spherical mass distributions?

We can't use Newton's law of gravity directly for non-spherical mass distributions because Newton's law assumes point masses or spherical symmetry, where all mass is concentrated at the center. For non-spherical distributions, the mass is spread out unevenly, and we can't assume it is concentrated at a single point. Therefore, we need to use calculus to break the mass into differential elements (dm) and integrate the tiny forces (dF) generated by each element to find the total gravitational force (F).

How do you integrate the gravitational force over a non-spherical mass distribution?

To integrate the gravitational force over a non-spherical mass distribution, follow these steps:

1. Break the mass into tiny differential elements (dm).
2. Calculate the tiny force (dF) generated by each differential mass using Newton's law of gravity.
3. Set up the integral of dF over the entire mass distribution.
4. Express the integral in terms of the given variables and constants.
5. Evaluate the integral to find the total gravitational force (F).

The integral is typically expressed as:

$F=GM\frac{\mathrm{dm}}{r^2}$

What are the steps to solve mass distribution problems using calculus?

To solve mass distribution problems using calculus, follow these steps:

1. Write the equation for the gravitational force (F) using the integral form.
2. Pick differential mass elements (dm) and write an expression for the distance (r).
3. Break the integral into its x and y components.
4. Expand the components into sines and cosines, and relate them to the given variables.
5. Plug in the expression for r and pull out constants from the integral.
6. Evaluate the integral to find the total gravitational force (F).

This method allows for accurate calculations of gravitational forces in non-spherical mass distributions.