Spinning on String of Variable Length: Videos & Practice Problems

In a system demonstrating conservation of angular momentum, a block spins on a table while connected to a hanging mass. As the radial distance decreases, the block's rotational speed increases, illustrating the relationship between angular momentum and RPM. The equations governing this system include mi>r1⁢RPM1=r2⁢RPM2. The tension from the hanging mass provides the necessary centripetal force, linking mass, velocity, and gravitational acceleration.

Spinning on a string of variable length

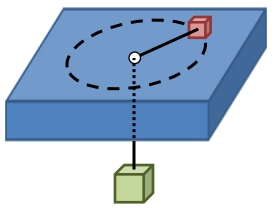
In this scenario, we explore the conservation of angular momentum through a system where a block spins on a horizontal table, connected to a hanging mass via a string that passes through a hole in the table. The block's motion is influenced by the tension in the string, which provides the necessary centripetal force for circular motion. As the length of the string decreases, the radius of the block's circular path also decreases, leading to an increase in its angular velocity.

Initially, the block has a mass of 2 kg and spins at 120 RPM when it is 10 cm (0.1 m) from the hole. To find the new RPM when the radius is reduced to 6 cm (0.06 m), we apply the principle of conservation of angular momentum, which states that the initial angular momentum equals the final angular momentum. This can be expressed mathematically as:

$$I_{\text{initial}} \omega_{\text{initial}} = I_{\text{final}} \omega_{\text{final}}$$

For a point mass, the moment of inertia \(I\) is given by \(m r^2\). Since we are working with RPM, we convert angular velocity \(\omega\) to RPM using the relationship:

$$\omega = \frac{2 \pi \text{RPM}}{60}$$

After substituting and simplifying, we arrive at the equation:

$$\text{RPM}_{\text{final}} = \text{RPM}_{\text{initial}} \left(\frac{r_{\text{initial}}^2}{r_{\text{final}}^2}\right)$$

Plugging in the values, we find that the new RPM is approximately 333 RPM, indicating that the block spins faster as the radius decreases.

Next, we calculate the linear tangential speed \(v_{\text{tan}}\) at this new RPM. The relationship between tangential speed and angular velocity is given by:

$$v_{\text{tan}} = r \omega$$

Substituting the new radius and the converted angular velocity, we find that the tangential speed is approximately 2.1 m/s.

Finally, to maintain the block's spinning at the new RPM, we need to determine the mass \(m_2\) of the hanging object. The tension in the string, which provides the centripetal force, is equal to the weight of the hanging mass:

$$T = m_2 g$$

Using the centripetal force equation, we can express this as:

$$T = m_1 \frac{v_{\text{tan}}^2}{r}$$

By equating the two expressions for tension and solving for \(m_2\), we find:

$$m_2 = \frac{m_1 v_{\text{tan}}^2}{g r}$$

Substituting the known values, we determine that \(m_2\) must be approximately 15 kg to maintain the block's spinning at the calculated RPM. This example illustrates the interconnectedness of angular momentum, centripetal force, and the effects of changing radius on rotational motion.

A small object (red, m) is on a smooth table top and attached to a light string that runs through a hole in the table. The other end of the spring attaches to a hanging weight (green, M). When the small object is given some speed, it spins in a circular path around the hole, with the tension from the hanging weight providing the centripetal force that keeps it spinning. If the object spins with angular speed ω when it is a distance R from the central role, what new angular speed (in terms of ω) does it have when this distance is halved? What new mass does the hanging weight need, in terms of M, to support a circular path at the new speed?

• A. ω_f = ¹/₄ω
• B. ω_f = ¹/₂ ω
• C. ω_f = 2ω
• D. ω_f = 4ω

Answer: (D)

Here’s what students ask on this topic:

What is the principle of conservation of angular momentum in a spinning system with a variable string length?

The principle of conservation of angular momentum states that in a closed system with no external torques, the total angular momentum remains constant. In a spinning system with a variable string length, such as a block on a table connected to a hanging mass, this principle is crucial. As the radial distance (length of the string) decreases, the block's rotational speed increases to conserve angular momentum. This is mathematically expressed as $I_i{\omega }_i=I_f{\omega }_f$, where $I_i$ and $I_f$ are the initial and final moments of inertia, and ${\omega }_i$ and ${\omega }_f$ are the initial and final angular velocities.

How does changing the radial distance affect the rotational speed of a block on a table?

Changing the radial distance in a system where a block spins on a table affects its rotational speed due to the conservation of angular momentum. As the radial distance decreases, the block's rotational speed increases. This is because the moment of inertia, which depends on the radial distance, decreases, and to conserve angular momentum, the angular velocity must increase. The relationship is given by $I_i{\omega }_i=I_f{\omega }_f$. Thus, a shorter radial distance results in a faster spin, demonstrating the inverse relationship between moment of inertia and angular velocity.

What role does the hanging mass play in the spinning system on a table?

The hanging mass in a spinning system on a table provides the necessary centripetal force to maintain the block's circular motion. The tension in the string, caused by the gravitational force on the hanging mass, acts as the centripetal force. This tension is crucial for keeping the block in its circular path. The force can be expressed as $T=m_{2}g$, where $m_2$ is the mass of the hanging object and $g$ is the acceleration due to gravity. The tension must equal the centripetal force required for the block's motion, ensuring the system's stability and allowing the block to spin at the desired speed.

How do you calculate the linear speed of a block in a spinning system with a variable string length?

The linear speed of a block in a spinning system with a variable string length can be calculated using the relationship between linear speed and angular velocity. The formula is $v=r\omega$, where $v$ is the linear speed, $r$ is the radial distance, and $\omega$ is the angular velocity. To find the linear speed, you need the current radial distance and the angular velocity, which can be derived from the rotational speed in revolutions per minute (RPM). By converting RPM to angular velocity using $\omega =\frac{2\pi \mathrm{RPM}}{60}$, you can then calculate the linear speed.

What factors determine the mass needed for the hanging object in a spinning system?

The mass needed for the hanging object in a spinning system is determined by the required centripetal force to maintain the block's circular motion at a specific rotational speed. The mass must provide enough tension in the string to match the centripetal force, which is calculated using $F=\frac{m{v}^2}{r}$, where $m$ is the block's mass, $v$ is the linear speed, and $r$ is the radial distance. The tension, equal to the gravitational force on the hanging mass, is $T=m_{2}g$. Solving for $m_2$ ensures the system's stability and desired rotational speed.