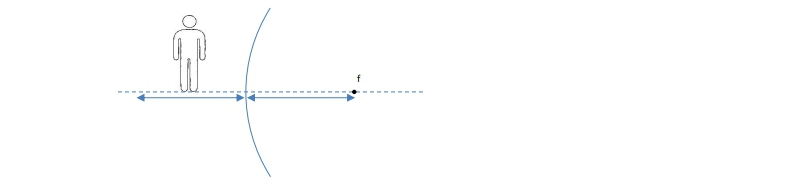
Ray diagrams are essential tools for understanding how light interacts with concave mirrors. These diagrams illustrate the path of light rays as they reflect off the mirror's surface, adhering to the law of reflection. A key point in these diagrams is the focus, denoted by the letter f, where collimated light rays converge after reflection. Collimated light refers to rays that are parallel before hitting the mirror.
To create a ray diagram for a concave mirror, you typically draw two specific lines. The first line is drawn parallel to the central axis; upon reflection, it will pass through the focus. Conversely, if you draw a line through the focus, it will reflect off the mirror parallel to the central axis. Additionally, a line drawn to the apex (or vertex) of the mirror reflects at the same angle it arrived, following the law of reflection.
When light from an object, such as a person, strikes the mirror, it forms an image. This image is defined as the convergence of light rays. To locate the image, you need to draw two of the three possible ray lines and find their intersection point. For example, if you draw a ray from the top of the person's head that reflects through the focus and another that goes through the focus and reflects parallel to the central axis, the intersection of these rays indicates the position of the image. Notably, if the convergence occurs below the central axis, the image will be inverted; if above, it will be upright.
Consider an object placed at the focal point of a concave mirror. In this scenario, drawing the necessary rays reveals that they do not converge. This is because the angles formed by the rays are equal, indicating that they will remain parallel after reflection. Consequently, no image is formed when the object is located at the focal point, as the rays do not intersect.
In summary, understanding ray diagrams for concave mirrors involves recognizing the significance of the focus, the behavior of light rays upon reflection, and the relationship between the position of the object and the resulting image. This knowledge is crucial for applications in optics and various technologies that utilize reflective surfaces.