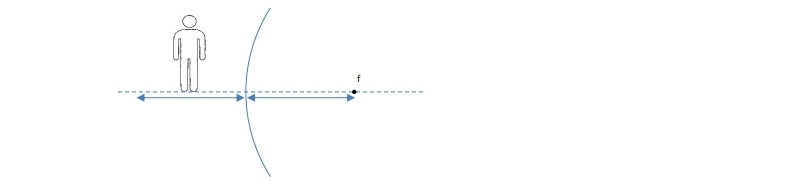
Ray Diagrams For Mirrors: Videos & Practice Problems

Ray diagrams illustrate how light interacts with different types of mirrors. For concave mirrors, light converges at a focal point, forming real images that can be inverted. In contrast, convex mirrors cause light to diverge, creating virtual images that appear upright and are located behind the mirror. Plane mirrors reflect light without convergence or divergence, producing virtual images of the same height as the object, positioned at an equal distance behind the mirror. Understanding these principles is essential for grasping concepts like focal length and the law of reflection.

Ray Diagrams for Concave Mirrors

Ray diagrams are essential tools for understanding how light interacts with concave mirrors. These diagrams illustrate the path of light rays as they reflect off the mirror's surface, adhering to the law of reflection. A key point in these diagrams is the focus, denoted by the letter f, where collimated light rays converge after reflection. Collimated light refers to rays that are parallel before hitting the mirror.

To create a ray diagram for a concave mirror, you typically draw two specific lines. The first line is drawn parallel to the central axis; upon reflection, it will pass through the focus. Conversely, if you draw a line through the focus, it will reflect off the mirror parallel to the central axis. Additionally, a line drawn to the apex (or vertex) of the mirror reflects at the same angle it arrived, following the law of reflection.

When light from an object, such as a person, strikes the mirror, it forms an image. This image is defined as the convergence of light rays. To locate the image, you need to draw two of the three possible ray lines and find their intersection point. For example, if you draw a ray from the top of the person's head that reflects through the focus and another that goes through the focus and reflects parallel to the central axis, the intersection of these rays indicates the position of the image. Notably, if the convergence occurs below the central axis, the image will be inverted; if above, it will be upright.

Consider an object placed at the focal point of a concave mirror. In this scenario, drawing the necessary rays reveals that they do not converge. This is because the angles formed by the rays are equal, indicating that they will remain parallel after reflection. Consequently, no image is formed when the object is located at the focal point, as the rays do not intersect.

In summary, understanding ray diagrams for concave mirrors involves recognizing the significance of the focus, the behavior of light rays upon reflection, and the relationship between the position of the object and the resulting image. This knowledge is crucial for applications in optics and various technologies that utilize reflective surfaces.

Will an image be formed for an object placed inside the focus of a concave mirror? If so, where will it be formed?

• A. The same distance behind the concave mirror.
• B. No image
• C. Yes, at focus
• D. Yes, at the center of curvature.

Answer: (B)

Ray Diagrams for Convex Mirrors

Ray diagrams for convex mirrors illustrate how light behaves when it reflects off these types of mirrors. Unlike concave mirrors, which converge light, convex mirrors cause light to diverge. This divergence means that light rays do not actually converge at a point; instead, they appear to originate from a virtual focus behind the mirror. This phenomenon is known as apparent focus, where the brain interprets the diverging rays as if they are converging at a point, creating the illusion of a focused image.

The focal length of a convex mirror is defined as the distance from the mirror's apex to this apparent focus. To construct ray diagrams for convex mirrors, you typically draw two of three essential rays. The first ray is drawn parallel to the principal axis and, upon reflection, diverges away from the focus. The second ray is directed towards the focus and, after reflection, travels parallel to the principal axis. The third ray, which is drawn from the apex of the mirror, reflects at the same angle as it was incident. This third rule remains consistent with both concave and convex mirrors.

When light from an object strikes a convex mirror, it forms a virtual image. This image is not real because the light does not converge; however, it appears upright and is located behind the mirror. For example, if an object is positioned at a distance equal to the focal length from the mirror, the ray diagram will show the apparent convergence of light, indicating the formation of a virtual image. This image will always appear upright and smaller than the actual object, reinforcing the unique properties of convex mirrors in applications such as security and vehicle side mirrors.

Find the location of the virtual image produced by a convex mirror when the object is placed a distance less than the focal length from the surface of the mirror.

• A. Distance less than f behind the mirror
• B. Distance less than f in front of the mirror
• C. A distance greater than f behind the mirror
• D. A distance greater than f in front of the mirror
• E. No image is formed

Answer: (A)

Ray Diagrams for Plane Mirrors

Plane mirrors, commonly found in bathrooms and on walls, are flat surfaces that reflect light without converging or diverging it. According to the law of reflection, when light rays strike a plane mirror perpendicularly, they reflect off at the same angle, maintaining their collimated nature. This means that plane mirrors do not have a focal point, either in front or behind the mirror. For mathematical purposes, the focal length of a plane mirror is often considered to be infinity, allowing for easier calculations in related equations.

When drawing ray diagrams for plane mirrors, two types of lines are essential: one that is parallel to the central axis and another that reflects off the mirror at the same angle as it hits. Unlike convex and concave mirrors, which have specific focal points, plane mirrors reflect light uniformly across their surface, making this principle applicable at any point on the mirror.

To illustrate the properties of plane mirrors, consider an example where a 1.6-meter tall person stands 0.7 meters away from a plane mirror. The image produced by the mirror will also be 1.6 meters tall and will appear to be located 0.7 meters behind the mirror. This image is classified as virtual because the light does not actually converge at that point; it only appears to do so. In fact, only concave mirrors can produce real images by converging light, while convex mirrors diverge light and cannot form real images. Thus, the characteristics of plane mirrors ensure that they always create virtual images that are upright, the same height as the object, and located at an equal distance behind the mirror as the object is in front of it.

You want to hang a plane mirror on your wall. If you want your entire body to fit into the mirror, what's the maximum height off the ground that the mirror must be? What is the smallest mirror you can buy? Consider yourself to be 1.55 m tall.

• A. Height of mirror = 0m; Size of mirror = 1.55m
• B. Height of mirror = 0.775m; Size of mirror = 0.775m
• C. Height of mirror = 0.775m; Size of mirror = 1.55m
• D. Height of mirror = 0.5m; Size of mirror = 0.775m

Answer: (B)

Here’s what students ask on this topic:

What is the difference between real and virtual images in ray diagrams for mirrors?

Real images are formed when light rays actually converge at a point after reflecting off a mirror. These images can be projected onto a screen and are typically inverted. Concave mirrors can form real images when the object is placed beyond the focal point. Virtual images, on the other hand, are formed when light rays appear to diverge from a point behind the mirror. These images cannot be projected onto a screen and are always upright. Convex mirrors and plane mirrors always form virtual images. Understanding the nature of these images is crucial for applications in optics and imaging technologies.

How do you draw ray diagrams for concave mirrors?

To draw ray diagrams for concave mirrors, follow these steps: First, draw a line parallel to the central axis from the object to the mirror. This ray will reflect through the focal point. Second, draw a line from the object through the focal point to the mirror. This ray will reflect parallel to the central axis. Lastly, you can draw a line from the object to the apex of the mirror, which will reflect at the same incident angle. The point where these reflected rays converge is where the image is formed. This method helps visualize how concave mirrors focus light to form images.

Why do convex mirrors only form virtual images?

Convex mirrors only form virtual images because they cause light rays to diverge after reflection. When parallel light rays hit a convex mirror, they spread apart as if they are emanating from a focal point behind the mirror. Since the reflected rays never actually converge, the image formed is virtual. This virtual image appears upright and smaller than the actual object, making convex mirrors useful for applications like vehicle side mirrors, where a wider field of view is beneficial.

How do plane mirrors form images?

Plane mirrors form images by reflecting light according to the law of reflection, where the angle of incidence equals the angle of reflection. The reflected rays appear to come from a point behind the mirror, creating a virtual image. This image is the same size as the object and is located at the same distance behind the mirror as the object is in front of it. Plane mirrors do not converge or diverge light, so the image is always virtual and upright. This principle is why plane mirrors are commonly used in everyday applications like bathroom mirrors.

What is the focal length of a concave mirror, and how is it determined?

The focal length of a concave mirror is the distance from the mirror's surface to its focal point, where parallel light rays converge after reflection. It is denoted by the letter f. The focal length can be determined using the mirror equation: $\frac{1}{f}=\frac{1}{\mathrm{d\_o}}+\frac{1}{\mathrm{d\_i}}$, where d_o is the object distance and d_i is the image distance. For a concave mirror, the focal length is positive, and it helps in determining the position and nature of the image formed.