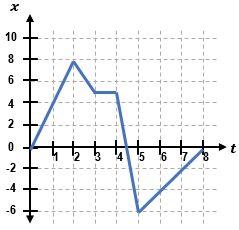
Position-Time Graphs & Velocity: Videos & Practice Problems

Position-time graphs illustrate an object's position over time, with the y-axis representing position and the x-axis representing time. The slope of the graph indicates velocity, where upward slopes signify forward motion, horizontal lines indicate a stop, and downward slopes represent backward movement. Curved graphs indicate changing velocity and non-zero acceleration. Average velocity is calculated between two points using the slope formula Δx × Δt, while instantaneous velocity is determined using a tangent line at a specific point.

Intro to Position-Time Graphs & Velocity

Position-time graphs are essential tools for visualizing the motion of an object, where the vertical axis represents position (denoted as x) and the horizontal axis represents time. Understanding how to interpret these graphs allows us to calculate important quantities like velocity. For instance, if an object moves 6 meters forward in 3 seconds, this motion can be represented on a graph by plotting the points corresponding to its position at each time interval.

To illustrate, if an object starts at the origin (0,0) and moves to (3,6) on the graph, this indicates it has traveled 6 meters in 3 seconds. If the object then remains stationary for 1 second, the graph will show a horizontal line from (3,6) to (4,6), indicating no change in position. Finally, if the object moves back to its starting point, the graph will depict a downward slope from (4,6) to (5,0).

The velocity of an object can be calculated from the slope of the position-time graph using the formula:

\( v = \frac{\Delta x}{\Delta t} \)

Here, \( \Delta x \) represents the change in position (the vertical change or "rise"), and \( \Delta t \) represents the change in time (the horizontal change or "run"). For example, if we analyze the segment from point A to point B, the slope can be visualized as a triangle where the vertical leg represents the change in position and the horizontal leg represents the change in time. A positive slope indicates forward motion, a horizontal slope indicates the object is stationary, and a negative slope indicates backward motion.

To calculate average velocities over specific intervals, one can identify the coordinates of the endpoints of each segment on the graph. For instance, if the object moves from a position of -10 meters to 10 meters over 2 seconds, the average velocity can be calculated as:

\( v_{avg} = \frac{10 - (-10)}{2 - 0} = \frac{20}{2} = 10 \, \text{m/s} \)

In contrast, if the object remains at the same position (10 meters) for the next 2 seconds, the average velocity is:

\( v_{avg} = \frac{10 - 10}{4 - 2} = \frac{0}{2} = 0 \, \text{m/s} \)

For a downward slope, such as moving from 10 meters to 5 meters in 1 second, the average velocity would be:

\( v_{avg} = \frac{5 - 10}{5 - 4} = \frac{-5}{1} = -5 \, \text{m/s} \)

To find the overall average velocity for the entire motion from 0 to 5 seconds, one can connect the initial and final positions on the graph. The average velocity for the entire interval can be calculated as:

\( v_{avg} = \frac{5 - (-10)}{5 - 0} = \frac{15}{5} = 3 \, \text{m/s} \)

It is important to note that the steepness of the slope on the graph correlates with the magnitude of the velocity; steeper slopes indicate higher velocities, while flatter slopes indicate lower velocities. The direction of the slope (upward or downward) indicates the direction of motion. Understanding these concepts is crucial for analyzing motion through position-time graphs.

The position-time graph for a moving box is shown below.

(a) What is the box's average velocity from 0 to 5s?
(b) What is the box's average velocity from 0 to 8s?
(c) What is the box's velocity in the interval where it's moving fastest?

• A. (a) 0 m/s; (b) 0 m/s; (c) 4 m/s
• B. (a) 4.4 m/s; (b) 3 m/s; (c) 11 m/s
• C. (a) -1.2 m/s; (b) 3 m/s; (c) 4 m/s
• D. (a) -1.2 m/s; (b) 0 m/s; (c) -11 m/s

Answer: (D)

Curved Position-Time Graphs & Acceleration

Position-time graphs can exhibit both straight lines and curves, each conveying different information about an object's motion. When a position-time graph is curved, it indicates that the object's velocity is changing, which implies that the acceleration is not equal to zero. In contrast, straight lines on a position-time graph signify constant velocity, meaning the acceleration is zero.

The slope of a position-time graph represents the velocity of the object. For straight lines, the slope remains constant between any two points, resulting in a consistent velocity. However, in a curved graph, the slope varies, indicating that the velocity is changing and thus there is acceleration present.

Understanding the sign of acceleration is crucial when interpreting curved graphs. A graph that curves upwards, resembling a smiley face, indicates positive acceleration. This occurs because the velocity transitions from negative to positive, suggesting that the object is speeding up. Conversely, a graph that curves downwards, resembling a frowny face, indicates negative acceleration, as the velocity shifts from positive to negative, meaning the object is slowing down.

Additionally, curves can be analyzed by dividing them into left and right sections. In the left section of a curve, the object is slowing down, as the slope becomes less steep, approaching zero. In the right section, regardless of whether the curve is a smiley or frowny face, the object is speeding up, as the slope becomes steeper, indicating an increase in velocity magnitude.

In summary, recognizing the characteristics of position-time graphs—whether they are straight or curved—allows for a deeper understanding of an object's motion, including its velocity and acceleration. This knowledge is essential for analyzing motion in physics.

Position-Time Graphs and Instantaneous Velocity

In analyzing motion through position-time graphs, it's essential to distinguish between average velocity and instantaneous velocity. Average velocity is calculated between two points on the graph, while instantaneous velocity refers to the velocity at a specific point in time. To find average velocity, one can draw a straight line connecting two points on the graph and determine the slope of this line, which is represented mathematically as:

Average Velocity \( v_{avg} = \frac{\Delta x}{\Delta t} \

where \( \Delta x \) is the change in position and \( \Delta t \) is the change in time. For example, if the position at \( t = 10 \) seconds is 30 meters and at \( t = 25 \) seconds is 60 meters, the average velocity can be calculated as follows:

\( \Delta x = 60 - 30 = 30 \) meters

\( \Delta t = 25 - 10 = 15 \) seconds

Thus, the average velocity is:

\( v_{avg} = \frac{30 \text{ m}}{15 \text{ s}} = 2 \text{ m/s} \)

On the other hand, instantaneous velocity is determined by the slope of a tangent line at a specific point on the graph. This tangent line touches the curve at only one point and represents the direction and steepness of the graph at that instant. For instance, to find the instantaneous velocity at \( t = 10 \) seconds, one would draw a tangent line at that point and calculate its slope using two nearby points. If the positions at these points are 15 meters and 45 meters, the calculation would be:

\( \Delta x = 15 - 45 = -30 \) meters

\( \Delta t = 10 \) seconds

Thus, the instantaneous velocity is:

\( v_{instantaneous} = \frac{-30 \text{ m}}{10 \text{ s}} = -3 \text{ m/s} \)

It's important to note that at the peaks and valleys of the position-time graph, the instantaneous velocity is zero. This is because the slope of the tangent line at these points is horizontal, indicating no change in position at that instant. For example, at \( t = 5 \) seconds, if the graph is at a peak, the instantaneous velocity would be:

\( v_{instantaneous} = 0 \text{ m/s} \)

Understanding these concepts is crucial for analyzing motion accurately, as they provide insights into how an object's velocity changes over time.

The position-time graph for a ball on a track is shown below.
(a) What is the ball's velocity at 4s?
(b) At what time(s) is the ball approximately travelling at -10m/s?
(c) From t = 3 to 7s, what is the sign of the acceleration?

• A. (a) +5 m/s; (b) t= 7 s; (c) negative
• B. (a) +5 m/s; (b) t= 8 s; (c) positive
• C. (a) +1 m/s; (b) t= 6 s; (c) negative
• D. (a) +1 m/s; (b) t= 3.5 s; (c) positive

Answer: (A)

Here’s what students ask on this topic:

What is a position-time graph and how is it used to determine velocity?

A position-time graph illustrates an object's position over time, with the y-axis representing position and the x-axis representing time. The slope of the graph indicates the object's velocity. An upward slope signifies forward motion, a horizontal line indicates a stop, and a downward slope represents backward movement. To determine velocity, you calculate the slope of the graph using the formula:

$\frac{\Delta x}{\Delta t}$

where $\Delta x$ is the change in position and $\Delta t$ is the change in time. This slope gives the average velocity over a time interval.

How do you calculate average velocity from a position-time graph?

To calculate average velocity from a position-time graph, you need to determine the slope of the line connecting two points on the graph. The formula for average velocity is:

$\frac{\Delta x}{\Delta t}$

where $\Delta x$ is the change in position (final position minus initial position) and $\Delta t$ is the change in time (final time minus initial time). This slope represents the average velocity over the selected time interval.

What does a curved position-time graph indicate about an object's motion?

A curved position-time graph indicates that the object's velocity is changing, which means there is acceleration. If the curve is upward (like a smiley face), the acceleration is positive. If the curve is downward (like a frowny face), the acceleration is negative. The changing slope of the curve shows that the velocity is not constant, and the object is either speeding up or slowing down depending on the direction of the curve.

How do you determine instantaneous velocity from a position-time graph?

To determine instantaneous velocity from a position-time graph, you need to find the slope of the tangent line at a specific point on the graph. A tangent line touches the graph at only one point and represents the velocity at that instant. The slope of this tangent line is calculated using the formula:

$\frac{\Delta x}{\Delta t}$

where $\Delta x$ is the change in position and $\Delta t$ is the change in time. This slope gives the instantaneous velocity at that specific point.

What is the difference between average velocity and instantaneous velocity?

Average velocity is calculated over a time interval between two points on a position-time graph, using the formula:

$\frac{\Delta x}{\Delta t}$

where $\Delta x$ is the change in position and $\Delta t$ is the change in time. Instantaneous velocity, on the other hand, is the velocity at a specific point in time and is determined by the slope of the tangent line at that point on the graph. While average velocity gives an overall rate of change, instantaneous velocity provides the rate of change at a particular moment.