Standing Waves - Online Tutor, Practice Problems & Exam Prep

Standing waves occur when waves interfere in specific patterns, creating nodes and antinodes. The fundamental frequency, denoted as f₁ = v2l, represents the simplest standing wave with one loop. Higher harmonics, or overtones, follow the relationship f_n = n⁢f₁. The wavelength for these waves is given by λ = 2l for the fundamental frequency, illustrating the relationship between frequency, wavelength, and wave speed.

Intro to Transverse Standing Waves

Guys, in earlier videos, we saw that waves can interfere with each other. In this video, I'm going to show you that in some cases, waves can interfere in a special way to produce a special type of wave called a standing wave. I'm going to introduce you to transverse standing waves on strings. Now there's a lot of conceptual information to understand here, but the hardest thing about standing waves is understanding what exactly is going on. I'm going to break it down for you guys and show you exactly what a standing wave is. To do that, I'm basically going to show you 3 different scenarios to understand what a standing wave is all about. Let's go ahead and take a look here.

So, what I want you to do is imagine that you have a string in your hand that you're whipping up and down and that the string is tied to a fixed end like a doorknob. Your oscillator, the thing that's moving up and down, is your hand and it's tied to the doorknob. Let's take a look at the first scenario here. You're going to take the string and whip it up just once. You're going to create a single pulse that moves to the right. What happens when that pulse actually reaches the doorknob? You have this pulse that reached the doorknob like this, and that disturbance has to go somewhere. Basically, the doorknob is going to flip this pulse upside down and now this pulse is going to be going backwards. In general, when a traveling wave reaches a fixed endpoint like a doorknob, it's going to create a reflected wave or pulse that travels backwards, but it's going to be inverted.

Now, let's take a look at the second one. Now you have the string and instead of whipping it up twice or once, you're just going to whip it up and down once to create a single wave. You're going to wait a few seconds and create another up and down to create two waves here. So you have two waves moving to the right. What happens later on? Well, basically the right wave is going to hit the doorknob first, and it's going to invert, and now it's going to travel to the left. The left wave is still moving to the right. So the left wave is going to be over here, and it's going to have traveled to the right like this, and you're going to end up with a wave pattern that looks like this. You have these two waves now that are sort of moving towards each other, and they're going to interfere. You end up with the superposition of these waves, and it's going to look something like this. It's going to look like a wave pattern. For most frequencies that you whip the string up and down, the waves are going to interfere somewhat randomly, creating a jumbled mess that does not create any sort of pattern.

Now, let's take a look at the third scenario. Change your frequency, go a little bit slower or faster, and what happens is that for very special frequencies, you're going to create some interesting patterns. If you slow down your wiggle and create a single arc that goes from left to right from your hand all the way to the doorknob, when it reaches the doorknob, it's going to flip upside down, it's going to go backwards like this. If you keep this frequency, you're basically going to create a wave that looks as if it's just going up and down, but it's not actually moving left to right. It kind of looks like a jump rope if you were to look at it from the side. For very special frequencies, you're going to create an interference pattern that's very special and you generate a wave that looks as if it's stationary. Because this wave looks as if it's standing still, we call it a standing wave. That's what a standing wave is. It's just a special wave pattern that you get for a very special frequency. This doesn't happen for all frequencies. As we saw in the second example here, for any sort of general frequency, you're going to create a jumbled mess of waves that interfere randomly.

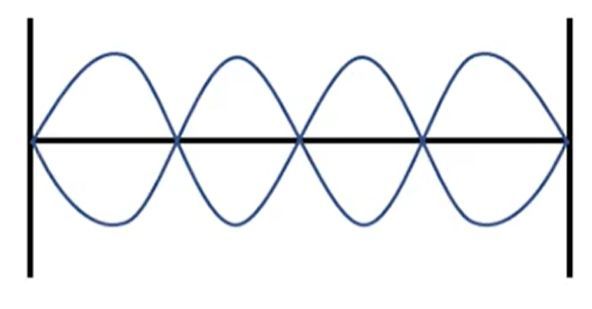
Let's talk about these frequencies. We said that there's a very special frequency, but there's actually an infinite number of these special frequencies that create standing waves. If I start off from this pattern here and I take the string and whip it up and down even faster, eventually, I'm going to create another pattern in which I have a single wavelength along the string. When it reaches the doorknob, it's going to invert and it's going to travel backwards, and you're going to create another standing wave pattern that's going to look like this. It's going to have this weird sort of loopy pattern. If you vibrate this even faster, you're going to create another standing wave pattern where you have three loops, then four and so on. Here, the letter \( n \) is the number of loops in our standing wave pattern. For the most basic one that we created, we have one loop, and for this one, we have two pairs of loops, and this is \( n = 2 \) and then you get \( n = 3 \), and so on.

The most important frequency that you need to know is called the fundamental frequency, which is given by the letter \( f_1 \). It's the frequency where \( n = 1 \). Anytime you see the fundamental frequency, it just means that \( n = 1 \). It's the frequency that you need to whip the string up and down so you can create this pattern right here, the most basic type of standing wave. The reason this fundamental frequency is important is that once you figure that out, you can actually figure out all of the other harmonic frequencies. Harmonic frequencies are just the other frequencies for all other standing wave patterns that you can possibly get where you have more than one loop, and they're basically just multiples of this fundamental one. The general equation you're going to see is that \( f_n \), for any number of loops, is just going to be \( n \times f_1 \).

Let's go ahead and take a look at an example here. We have a string between two supports and it vibrates in a standing wave pattern. We have three loops right here. In the first part, we want to draw a sketch of the wave. So for this first part here, we have \( n = 3 \). What does it tell us? Remember, \( n \) is just the number of loops. We have three loops where we have \( n = 3 \). A sketch of this wave would look like this. We're going to have one loop, this is going to be the second loop, and this is going to be the third one. The frequency of the standing wave pattern is 15 Hertz. Because \( n = 3 \), what they're saying is that \( f_3 \) is equal to 15 Hertz. Now, in the second part, we are asked to find out what the fundamental frequency is. Remember, anytime you see the word fundamental, what that means is that \( n = 1 \). If \( n = 1 \), what they're asking us is what is \( f_1 \) right here? Using the equation \( f_3 = 3 \times f_1 \), we can solve for \( f_1 \), which is \( 15 \div 3 = 5 \) Hertz. To create a standing wave pattern with three loops, you'd have to vibrate the string up and down at 15 Hertz. But to create a standing wave pattern with just one loop, you'd have to slow down that frequency and pulse the string at 5 Hertz to create a more simple wave pattern. Now let's look at the frequency for a standing wave with five loops. They're stating that \( n = 5 \). So what is \( f_5 \)? We're going to use this equation right here, \( n \times f_1 \). So the idea here is that you'd have \( 5 \times 5 \) Hertz, and you get 25 Hertz. Every time you add 5 Hertz, you vibrate the string 5 Hertz faster, and you end up with one more loop in your standing wave pattern. That's it for this one guys. Let me know if you have any questions.

By whipping a string up and down, you determine the fundamental frequency to be 4 Hz. If you attached the string to a motorized oscillator and increased the frequency to 28 Hz, how many loops would this standing wave have?

• A. 14
• B. 4
• C. 28
• D. 7

One of the harmonic frequencies for a particular string under tension is 325 Hz. The next higher harmonic frequency is 390 Hz. What harmonic frequency is next higher after the harmonic frequency 195 Hz?

• A. 260 Hz
• B. 130 Hz
• C. 196 Hz
• D. 4 Hz

Equations for Transverse Standing Waves

Everyone, welcome back. So in the last couple of videos, I showed you the basics of standing waves, and I showed you what sort of what they look like on a graph. So imagine that you had a string set up between these two supports, and you had some kind of a frequency to set up a standing wave. It would look like this. You'd see a wave kind of like bouncing up and down. And then if you increase the frequency, you would end up with another standing wave with 2 loops where it would kind of look like this, and that would be a certain frequency. And then n=3, there'd be 3 loops and so on and so forth. And in those types of problems, we were actually already given what the fundamental frequencies are. Well, in this video, I'm gonna show you the equations for actually those transverse standing waves. How do we actually find out what frequency and wavelength and all those things are when they're not given to us? We're gonna see actually a couple of examples and a couple of equations. There's actually really only one equation that you have to learn, and then we'll do it a couple of examples together. Let's get started. Alright. So just remember that standing waves can only exist for special harmonic frequencies, and we have special values for the wavelength. Alright? I'm just gonna go ahead and actually give you these equations. The first frequency, which is n=1, remember that's called the fundamental frequency, is actually just given by v=v÷2l. We can actually figure out this out just by looking at the properties of the string and the wave itself. Alright? So, remember that the harmonic frequencies are just if we took fone1 and we just multiplied it by some integer n, where n could equal 1 or 2 or 3, depending on how many loops we were looking at. Right? So in other words, we're just going to stick an n in front of that equation. And so I basically could just take this equation and generalize it. This is nv÷2l. All right? Now we can take this equation and figure out what the wavelength is, and what you're actually gonna see is that it's 2l÷n. You can actually really quickly see this because remember that the relationship between speed, frequency, and wavelength is v=λf. So if you actually use this equation to solve for λ, what you're going to see is that the v will cancel out, and all you're left with is that this sort of, the equation is flipped from the fundamental frequency. All right? So these are really just the 3 equations you'll need to go ahead and solve problems. And if you actually look at it, this is the only one you really need to remember because from this one, you can actually figure out what this is and also what this is. So let's go ahead and just jump right into our first problem over here. We're going to take a look at this example where we have a 1.5 meter long string that's stretched between these two supports, So l=1.5. And we know what the speed of these waves is going to be. We know what the speed of waves is going to be 48 meters per second. So in this first problem here, we're gonna figure out what is the wavelength and frequency of the fundamental tone. How do we do that? Well, basically, the fundamental tone here is gonna be when n=1. So when n=1, we're just trying to figure out the λ, which is gonna be 1 over here. And We can actually just use our equation for now. Right? Or now for this. So this is just gonna be 2l÷n, in which n is just equal to 1. So what's the 2l? This is just gonna be 2 times the length of the string, 2×1.5, and you get 3 meters. Alright? So that's the first answer. Now you might be thinking of this number, and you might be wondering, how can the wavelength be 3 meters when the length of the string is only 1.5? And remember what the fundamental frequency looks like. That's sort of the most basic type of frequency. We can only set up a standing wave with one loop. Alright? And so basically, what's going to happen is that the loop is kind of just going to bob up and down like this. But remember, this sort of up pattern like this is only half of what a full wavelength is. A full wavelength goes up and down and up again. Alright? So this only represents one half of that wave. So that's why the full wavelength of this wave over here is actually 3 meters even though the string is only 1.5. Alright? So that actually perfectly makes sense because if you if you continued on, that would be a full wavelength. Alright. So that's 3 meters. So now let's take a look at f1, the fundamental frequency. You can actually figure out a couple of different ways. You could use this equation over here, or we could just stick to the 2 equations that directly give us f1. So this is actually just going to be v÷2l, and which this this is going to be 48 divided by 2 times 1.5. What What you're gonna get here is that this is 16 hertz. Alright? That's gonna be 16 hertz. So now let's take a look at the next equation over here, the next problem. The next problem says we're gonna take a look at the wavelength and frequency of the first overtone. What does that mean? Well, it turns out that there's actually 2 special words that will actually directly tell you what the value of n is. We've already taken a look at harmonic. Right? Harmonic just means basically, that's what the n value is. For example, the first harmonic is where n=1. So it's basically just telling you n=1. 2nd harmonic is when n=2. 3rd harmonic equals n=3, so on and so forth. So whatever the harmonic is, that's what n is. But the word overtone is something you might see, and it's kinda complicated or it's kinda just tricky because, really, what that means is an overtone is n tones over the fundamental frequency. So, for example, the second harmonic is when n=2, but that's also the first overtone because it's the first tone over the fundamental frequency. So n=2 is the second harmonic, but it's the first over tone. n=3 is the 3rd harmonic, but it's the second overtone, and so on and so forth. So when they're asking for the first overtone, really, what they're actually cluing you in on is that n=2. Alright? So we're just going to solve these exact same, same values, λ and f. Well, now we're just going to look at when n=2. Alright? This is going to be λ2. And again, I can just use this formula over here. This is going to be 2l÷2. In other words, that will cancel out and all we'll just be left with is l, and this is going to be 1.5 meters. So that's the wavelength here. Why does that make sense? Because remember, what n=2 is going to look like is it's gonna look like sort of a wave. It's gonna look like this. So it's gonna look it's gonna look like an up and down, which is gonna be a complete wave, and that's why the wavelength is equal to the length of the string. So that's going to be 1.5. And then finally, over here, we can see that f2 is just going to be remember, we can use nv÷2l, which case we're going to have 2×48÷2×1.5. We also could have just used n×fone because we already know what the fundamental frequency is. Either way, what you're actually gonna get here for an answer is that this is equal to 32 Hertz. Alright? So those are your answers for the, wavelength and frequencies of the fundamental and also the first overtone. Let me know if this makes sense, and thanks for watching. I'll see you in the next one.

The figure below shows a standing wave on a 2.0-m-long string that has been fixed at both ends and tightened until the wave speed is 40 m/s. What is the frequency of this wave?

• A. 20 Hz
• B. 160 Hz
• C. 40 Hz
• D. 10 Hz

Example 1

What's up, everyone? So let's see if we can work this example problem out together. We're gonna put together a lot of information that we've seen from waves and standing waves in this problem. Let's break it down. So we have a string that's fixed at both ends. It's 8 meters long and has a mass of 0.2 kilograms. So in other words, I'm told that the length is 8 and \( m \) is 0.2. What I'm also told is that this is a string, and it's subjected to a tension of 100 newtons. Now we've seen tension before in these types of problems with waves and strings, and that's the variable \( F_t \). So in other words, the force of tension on the string is 100 newtons. So the first thing we want to figure out in part a is the speed of waves on the string. That's just the wave speed. So let's put these things together and see if we can look at part a over here. Now remember, we have a couple of equations for velocity, but for strings, particularly, we had one equation, which is the square root of tension over \( \mu \). That's what we're gonna take a look at here because that applies to strings only, in this case, in transverse waves. So let's take a look at this \( v \) equation. Now remember, the \( \mu \) is the linear mass density. And just so for your recollection, it's the linear mass density is really just the mass divided by the length. That's what that \( \mu \) value becomes. Alright? If I just go ahead and plug all this stuff into my calculator, this is really just gonna be \( 100 \) divided by, the mass, which is \( 0.2 \) divided by the length, which is \( 8 \). If you plug all that stuff into your calculator, what you should get is a velocity of \( 63.2 \) meters per second. Alright? So that's the first part. So figuring out just the speed of waves that, sort of behave or as they move along on this on the string here. Alright?

Let's move on now to the second part. The second part asks us to find what is the longest possible wavelength for a standing wave. So what does that mean? What's the longest possible wavelength? Well, remember that the first loop, the \( n = 1 \), is actually basically like it's only just one bump up like this. Right? Whereas the \( n = 2 \), that's where you actually have 2 loops. And remember, that's gonna look like a standing wave like this. It's gonna look something like this, and then it's gonna basically just fold back over itself. So you're gonna have 2 loops like this. The \( n = 3 \) is gonna look like 3 loops, so it's gonna look a bit like this \( 1, 2, \) and then \( 3 \). Alright? Which one is the longest possible wavelength? Well, as the ends get bigger and bigger, you have more and more loops, which means that the wavelengths actually get shorter. Notice how the wavelength for \( n = 1 \) involves one complete cycle; it is actually only \( 1/2 \) of the wavelength, so to calculate the wavelength for \( n = 1 \), you're actually not gonna use an equation. You'll actually just see that it actually has to be double the length of the string. So, \( \lambda_1 \) is going to be equal to \( 16 \) meters. This will always be true. The longest possible wavelength of a standing wave will always correspond to \( n = 1 \) always.

Now, we're going to calculate the frequency of that wave. There are a couple of different ways to do this, but one of the easiest ways is to use the equation \( f_1 = v / 2l \). Let's use our wave speed, which we already know as \( 63.2 \) meters per second, calculated earlier in the problem, and divide it by \( 2 \times 8 \), the length of the string. The fundamental frequency you'll calculate should be \( 7.9 \) hertz. Alright? So those are the 3 parts of this problem: figuring out the wave speed, figuring out the longest possible wavelength, and what the corresponding frequency will be, and that actually happens to be the fundamental frequency. Let me know if that made sense. Thanks for watching, and I'll see you in the next video.

A 3m-long rope is stretched between two supports with a tension that makes the speed of transverse waves 60 m/s. What are the wavelength and frequency of the second overtone?

• A. $\lambda=2m;f=30Hz$
• B. $\lambda=1m;f=60Hz$
• C. $\lambda=3m;f=20Hz$
• D. $\lambda=6m;f=10Hz$