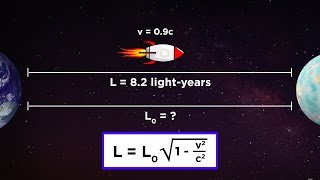35. Special Relativity
Consequences of Relativity
Learn with other creators
Practice this topic
- Multiple Choice
The international space station travels in orbit at a speed of 7.67 km/s. If an astronaut and his brother start a stop watch at the same time, on Earth, and then the astronaut spends 6 months on the space station, what is the difference in time on their stopwatches when the astronaut returns to Earth? Note that 6 months is about 1.577 x 107 s, and c = 3 x 10 8 m/s.
980views8rank2comments - Multiple Choice
In the following figure, a right triangle is shown in its rest frame, S'. In the lab frame, S, the triangle moves with a speed v. How fast must the triangle move in the lab frame so that it becomes an isosceles triangle?
945views3rank1comments - Multiple ChoiceCarol is in the same reference frame with a clock. Bianca is flying past Carol and her clock at a high speed. Bianca sees Carol's clock ticking at one quarter the rate that Carol sees. How fast is Bianca flying relative to Carol?936views
- Multiple ChoiceCarl is standing in a park 1000 m across. Rohan flies over the park at a very high speed, first passing over the east end of the park, and then passing over the west end. Carl and Rohan are discussing the time interval between when Rohan passed over the east end of the park and when he passed over the west end of the park. Who measured the proper time?802views
- Textbook Question
Your job is to synchronize the clocks in a reference frame. You are going to do so by flashing a light at the origin at t = 0 s. To what time should the clock at (x, y, z) = (30 m, 40 m, 0 m) be preset?
81views - Textbook Question
Bjorn is standing at x = 600 m. Firecracker 1 explodes at the origin and firecracker 2 explodes at x = 900 m. The flashes from both explosions reach Bjorn's eye at t = 3.0 μs. At what time did each firecracker explode?
882views - Textbook Question
A proton is accelerated to 0.999c. By what factor does the proton's momentum exceed its Newtonian momentum?
79views - Textbook Question
What are the rest energy, the kinetic energy, and the total energy of a 1.0 g particle with a speed of 0.80c?
111views