21. Kinetic Theory of Ideal Gases
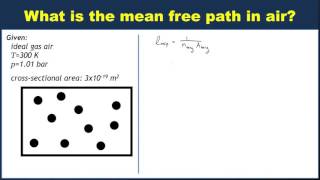
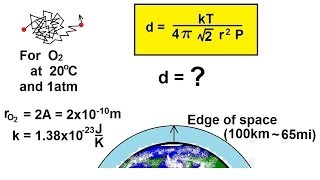
Mean Free Path of Gases
21. Kinetic Theory of Ideal Gases
Mean Free Path of Gases
Additional 4 creators.
Learn with other creators
Showing 7 of 7 videos
Practice this topic
- Multiple Choice
Laboratory environments can achieve pressures of 3.5×10-13 atm and temperatures of 300K. Calculate the mean free path (in km) of air molecules, which you can assume are diatomic.
398views3rank - Textbook QuestionCalculate the mean free path of air molecules at 3.50 * 10^-13 atm and 300 K. (This pressure is readily attainable in the laboratory; see Exercise 18.23.) As in Example 18.8, model the air molecules as spheres of radius 2.0 * 10^-10 m.1494views
- Textbook QuestionOn earth, STP is based on the average atmospheric pressure at the surface and on a phase change of water that occurs at an easily produced temperature, being only slightly cooler than the average air temperature. The atmosphere of Venus is almost entirely carbon dioxide (CO₂), the pressure at the surface is a staggering 93 atm, and the average temperature is 470℃. Venusian scientists, if they existed, would certainly use the surface pressure as part of their definition of STP. To complete the definition, they would seek a phase change that occurs near the average temperature. Conveniently, the melting point of the element tellurium is 450℃. What are (a) the rms speed and (b) the mean free path of carbon dioxide molecules at Venusian STP based on this phase change in tellurium? The radius of a CO₂ molecule is 1.5 x 10⁻¹⁰ m.355views
- Textbook QuestionPhotons of light scatter off molecules, and the distance you can see through a gas is proportional to the mean free path of photons through the gas. Photons are not gas molecules, so the mean free path of a photon is not given by Equation 20.3, but its dependence on the number density of the gas and on the molecular radius is the same. Suppose you are in a smoggy city and can barely see buildings 500 m away. a. How far would you be able to see if all the molecules around you suddenly doubled in volume?430views
- Textbook QuestionA mad engineer builds a cube, 2.5 m on a side, in which 6.2-cm-diameter rubber balls are constantly sent flying in random directions by vibrating walls. He will award a prize to anyone who can figure out how many balls are in the cube without entering it or taking out any of the balls. You decide to shoot 6.2-cm-diameter plastic balls into the cube, through a small hole, to see how far they get before colliding with a rubber ball. After many shots, you find they travel an average distance of 1.8 m. How many rubber balls do you think are in the cube?363views