Two wooden blocks are connected using an inelastic wire. The blocks are placed on a horizontal floor. The mass of block P is m_P while block Q has a mass m_Q. You pull the blocks to the left using a horizontal force F, giving the blocks a constant velocity. The coefficient of kinetic friction between both blocks and the surface is μ_k. Determine the tension in the wire connecting the blocks in terms of m_P, m_Q, and μ_k with the help of one or more free-body diagrams.

Mike is working as a helper in an appliance showroom. He is trying to pull a 25 kg refrigerator with a force of 125 N but he is unable to move it. Determine the force of friction acting on the refrigerator if the coefficient of static friction between the refrigerator and the showroom floor is 0.60.

A box of mass 3.0 kg is attached to an iron ball having mass 3.5 kg through a massless string passing over a frictionless pulley. Consider the system is initially at rest when the iron ball is suddenly released. Determine how much tension is developed in the string and also the acceleration experienced by the box.

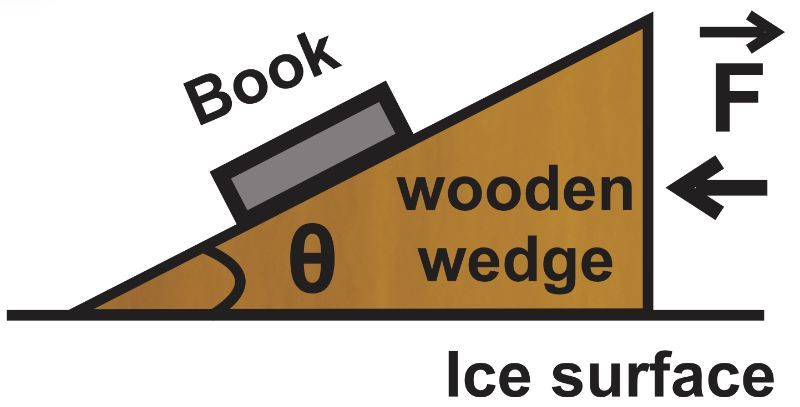
A 2.0 kg book rests on the rough, sloping surface of a wooden wedge of mass 5.0 kg, which itself lies on a frictionless ice surface as shown in the diagram below. If the coefficient of static friction between the book and the wooden wedge is μ=0.4 and $\theta$ = 25°, determine the minimum horizontal force F applied to the wooden wedge that will cause the book to start sliding up the incline.

A crate of mass m is connected to a stone weighing 5.0 kg through a massless string and a frictionless pulley as shown in the figure. Determine the value of 'm' that will keep the system moving at a constant speed if μ_k = 0.18 and μ_s = 0.42 are the coefficients of friction between the crate and the surface.

A 3.0 kg crate is on a 5.0 kg crate that is sliding on the horizontal floor at an acceleration of 1.1 m/s². It was found that for the minimum value of μ = 0.11 between the two crates, the crate on top wouldn't slide off on the crate at the bottom. If μ is only one-third of this value, what is the acceleration of the 3.0 kg crate relative to the 5.0 kg crate? (Assume μ = μ_s = μ_k)