A grandfather clock with a 1.00 m long pendulum hangs on a clock tower. The mass of the bob on the pendulum is 0.500 kg. An unlucky driver hits the tower vibrating it. If the pendulum was initially at rest in the equilibrium position, how many cycles per second will the pendulum make?

A decorative pendulum on a wall clock is made of a 250 grams gold coated spherical mass hanging on a 35 cm long lace. The homeowner starts the pendulum at 4:00 pm by giving it a displacement of 3.0 cm on one side. The pendulum is nearly perfect, with a damping constant of 2.5 * 10^-5 kg/s. Find the amplitude and number of cycles the pendulum makes by 11:00 pm.

Imagine a spherical ball with a mass of 296 g attached to a 0.64 m long string hanging from the ceiling. The ball is released at an angle of 14° to the vertical. Assuming the motion is simple harmonic, calculate the frequency at which the ball oscillates.

Imagine a metal ball suspended by a string, swinging back and forth at a certain frequency (f). Now, if we were to place this entire setup in an elevator descending with an acceleration of 0.28g, what would be the new frequency (f') of the ball's oscillations?

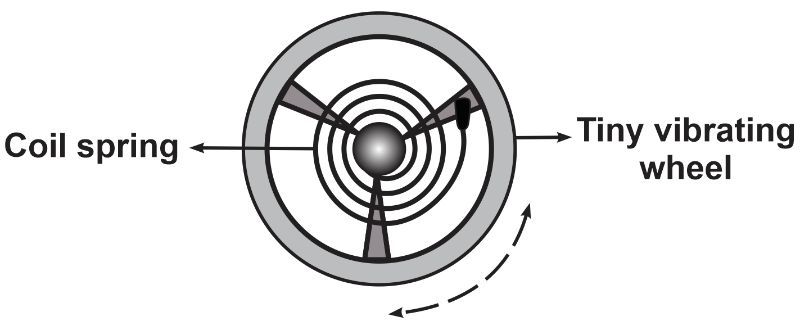
In a clock mechanism, a 0.96 cm radius pendulum wheel attached to a coil spring vibrates at 3.20 Hz. If 2.1 × 10⁻⁵ N.m torque causes a 60° rotation, what is the wheel's mass?

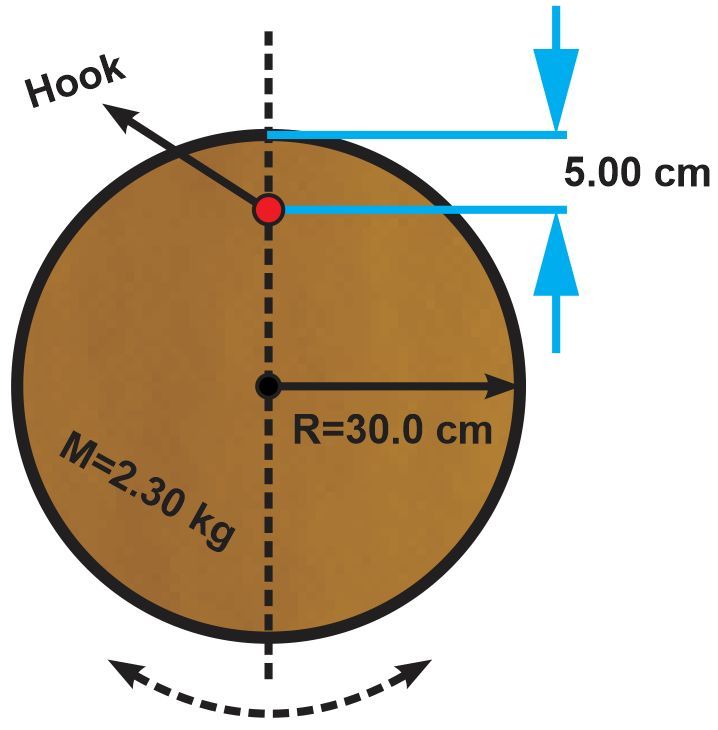
A 2.30 kg acrylic disk with 30.0 cm radius is suspended by a metal hook through a hole 5.00 cm from its edge, allowing it to swing as a pendulum. What is the period of its small oscillations?

An inventor makes a device consisting of a speaker hanging freely from the ceiling by a string. The speaker if set swinging, plays a drumbeat each time it reaches the maximum distance from the equilibrium. Given that the speaker plays 120 bpm (beats per minute) after it is set swinging, what is the length of the string?