Coins can be treated as discs. A dummy coin has an inner uniform solid disc with a diameter of 120.0 cm and an area density of 4.00 g/cm², which is encircled by a concentric ring with inner and outer diameters of 120.0 cm and 160.0 cm respectively and an area density of 2.50 g/cm². Find the coin's moment of inertia around an axis that passes through its center and is perpendicular to its plane.

A rectangle measures 30 cm by 50 cm. Point masses weighing 420 g are fitted on each of the four corners. Assume the connecting rods between the point masses have negligible mass. Find the moment of inertia of the system about an axis perpendicular to the square and passes through i) one of the corners and ii) the center of the short edge (point p).

There are two tiny balls affixed to the ends of a uniform bar. The balls can be thought of as point masses and have masses of 0.300 kg each, whereas the bar is 2.00 m long and has a mass of 4.00 kg. Find the combination's moment of inertia around an axis that passes through the middle of the bar and is perpendicular to it.

What is the moment of inertia of a thin uniform rod with two point masses attached to it and rotating about the axis shown in the figure?

An industrial conveyor belt is designed to transport packages to different processing areas within a facility. Along one section of the conveyor, five identical packages are placed at equal intervals, L, on a lightweight frame that can be considered massless. Each package has a mass of M. For maintenance purposes, the entire section can be rotated about a vertical axis passing through the package at the rightmost end, perpendicular to the length of the conveyor. Calculate the moment of inertia of the five packages about this axis of rotation.

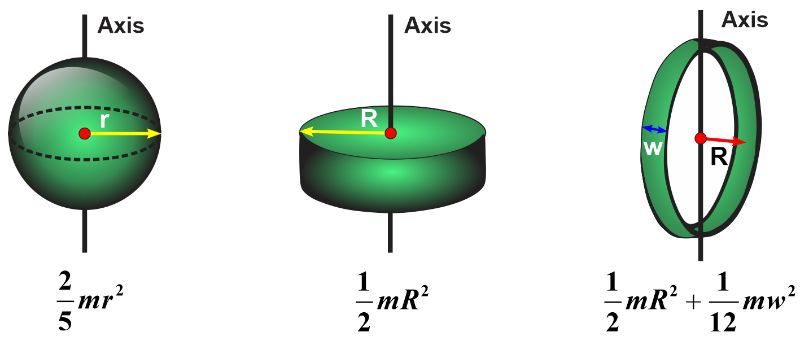
Sometimes, it is advantageous to calculate the moment of inertia with the radius of gyration k. This is defined as the perpendicular distance from the rotation axis at which, if all of the mass of the object is concentrated, the moment of inertia would be the same as the moment of inertia of the actual object. In other words, the moment of inertia of an object is simply I = mk². In light of this definition, find the radius of gyration of the solid sphere, the hoop, and the solid cylinder in the figure below.

What is the approximate distance between two nitrogen atoms in a diatomic nitrogen molecule, if the total mass of the molecule is 4.6 x 10⁻²⁶ kg and the moment of inertia around an axis perpendicular to the bond at the midpoint is 1.4 x 10⁻⁴⁶ kg•m²?