A freezer operating on the basis of the Carnot cycle has a constant temperature of 255 K. In each cycle, the freezer engine discards 600 J of heat in the kitchen. The kitchen has a temperature of 300 K. The freezer completes 220 cycles per minute. What is the power (P) required to maintain a constant temperature in the freezer?

A gasoline engine is installed in a car to convert chemical energy into mechanical work. It operates by repeating a cycle of four stages. At each cycle, it releases 3500 J of heat while generating 1700 J of mechanical work. Determine how much heat (Q_H) should be provided to the engine at each cycle.

Data center servers are cooled by a cooling system. The cooling system works between a cold room at 5℃ and a hot room at 50℃. A 40 cm long steel bar with a diameter of 3.3 cm connects the rooms. The cooling system extracts heat from the cold room at the same rate that it is transferred through the steel bar. Compute the required power input, in watts, for the cooling mechanism to achieve this heat extraction rate. The cooling system operates on the basis of the Carnot cycle and the thermal conductivity of steel is 45 W/m•K.

A cooling unit operates with a Carnot cycle between -15°C and 30°C. Find how much (i) heat is dissipated into the surrounding environment and (ii) energy must be supplied to the cooling unit in order to bring 18 kg of a liquid substance from 30°C to its solidification point at 5°C. Its latent heat of fusion (L_f) is 2.34 × 10⁵ J/kg.

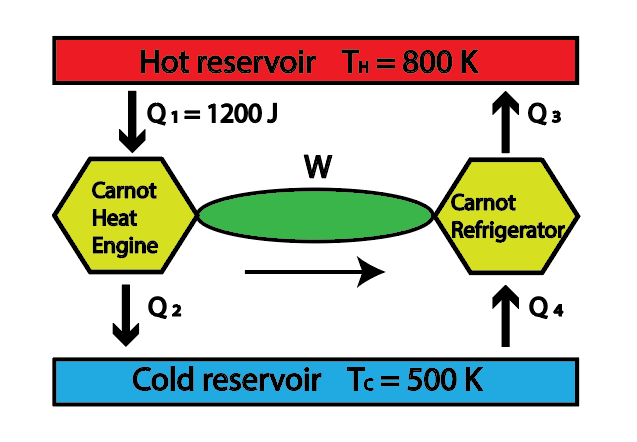
In the combined system in which a Carnot heat engine powers a Carnot refrigerator, the heat absorbed from the hot reservoir Q₁ is 1200 J. The hot reservoir has a temperature of 800 K, while the cold reservoir has a temperature of 500 K as shown in the figure. Determine the heat transfer values Q₃ and Q₄ for this interconnected arrangement.