A spring-mass system is used to simulate the motion of the human hamstring. The hamstring executes a simple harmonic with an amplitude of 15 cm and an angular frequency of 6.28 rad/s. Calculate I) i) the maximum magnitude of the acceleration and ii) the speed at the equilibrium position; II) i) the acceleration and ii) speed at the position x=-7.5 cm; III) the time needed to go directly from x=0 cm to x=+7.5 cm IV) Which of the quantities requested previously can be determined using the conservation of mechanical energy?

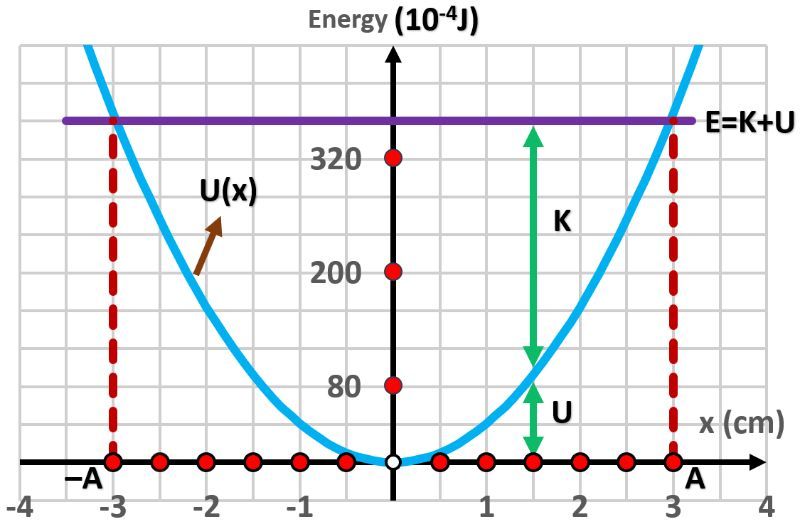
Consider a proton that is confined within a one-dimensional harmonic oscillator potential. The oscillator has a spring constant of 1.5 N/m. Determine the energy values corresponding to the first three levels of the proton's energy within this system.

Express the kinetic and potential energy in terms of the total energy for a horizontal spring in simple harmonic motion. Consider the displacement of the mass is C/5, where 'C' is the amplitude.

Suppose you have two masses, one of 300 g and the other of 400 g, connected to each other by a spring with a spring constant of 3.0 N/m. The masses are attached to walls via springs having a spring constant of 20 N/m. Initially, the 300 g mass is displaced 10 cm to the right and released, while the 400 g mass is at rest at the equilibrium position. Assuming no friction, how long will it take for the 300 g mass to stop moving and for the 400 g mass to start moving?

A 3.25-kg block is attached to the free end of a horizontally oscillating spring. The other end of the spring is attached to a wall. The position x of the block from the equilibrium position is given by the equation x = (0.540)cos(3.20t), where x is measured in meters and t is in seconds. Calculate the total energy of the system, assuming there is no energy dissipation.

A student is constructing a device for an exhibition at a science expo. It consists of an inclined plane at the foot of which a spring is attached. For testing the device, the student takes a billiard ball of 170 g and puts it at the free end of the spring. She compresses the spring by 9.0 cm and releases. Given that the incline makes an angle of 33° with the horizontal, the radius of the billiard ball is R = 6.0 cm and the speed at which the billiard ball is launched by the spring is 4.0 m/s, determining the spring constant of the spring. [Assume that the billiard ball rolls without slipping.]

Engineers are measuring the properties of suspension springs that are made in a factory. They fix one end of a sample spring to a wall and attach a block of 80 g to the other end. Then they make it oscillate with an amplitude of 3.0 cm. They find that the spring constant of the sample spring is 80 N/m. A computer generates its potential energy versus position graph that looks like the figure below. From the graph, find the potential energy of the spring corresponding to x = 2.0 cm. Assume that that friction is negligible and the spring is massless.

A floating cylinder undergoes SHM with an amplitude of 0.6 cm. The angular frequency of the motion is 4.45 rad/s, while the phase constant is π/3 rad. Draw about 2 cycles of the cylinder's velocity-time graph starting at t = 0s. Assume the motion follows x(t) = Acos(ωt +  ϕ).

The graph below is a position-time representation of the SHM of a floating block dipping and rising in water. Find its peak speed.