A weather satellite is in geostationary orbit, 36000 km above the equator. The satellite rotates around the earth at the same rate as the earth does. The satellite monitors the weather evolution of the same region of the earth using ultrasensitive detectors. Calculate the speed and acceleration of the satellite. The Earth's equatorial radius is 6378 km.

The radius of Mars is 3,389.5 km and rotates once every 24.6 hours. The radial acceleration at the equator must be larger than g for items to leave the surface of the planet and enter space. What would be the needed rotational period on Mars for this to happen? (g on the surface of mars is 3.7 m/s²)

Consider a Ferris wheel rotating in the vertical plane, with the position of a cabin modeled as a point moving in a circular path. The position in the xy-plane is given by $\vec{r}=(15.0\mathrm{\ m})\cos [(0.500\ \mathrm{rad}/\mathrm{s})t]\hat{i}+(15.0\mathrm{\ m})\sin [(0.5\mathrm{00\ rad}/\mathrm{s})t]\hat{j}$ , where r is in meters, and t is in seconds. Calculate the velocity and acceleration of the cabin as functions of time.

Gravity has very similar effects to acceleration. However, large accelerations are not so nice to human beings. Scientists have been conducting research on the effects of large accelerations on human beings. Suppose a person with a height of 1.72 m is centrifuged to a maximum acceleration of 9g using a horizontal arm that is 7.50 m long. Assuming the head of the person is positioned at the outermost end of the centrifuge arm, calculate the required rev/min to generate an acceleration of 9g.

Imagine an electron (mass m = 9.1 × 10^-31 kg) revolving around the nucleus of a helium atom, held in orbit by the electric force between them. At a distance of 0.5 × 10^-10 m, this electron experiences an electric force of 1.84 × 10^-7 N. Determine the number of revolutions per second that this electron makes around the nucleus.

You are riding a roller coaster that has a 60 m-diameter circular loop with a top speed of 25 m/s. What is your apparent weight at the bottom of the loop if your mass is 50 kg? What is your apparent weight at the top of the loop if the roller coaster's speed has decreased to 20 m/s?

A 5.0 kg object is attached to one end of a rod which has negligible mass. The object moves in a uniform circular motion in a vertical circle of radius 2.0 m. If the period of revolution is 1.2 s, calculate the speed of the object while it is revolving.

Ali wants to test the hypothesis that the weight of an object varies depending on its location. For this purpose, he measures the weight of a book (m = 10 kg) at the North Pole and the Equator. Assuming the Earth to be spherical, will the scale readings be the same or different?

During a washing cycle, the 40 cm diameter drum of a washing machine rotates about a horizontal axis. A child put her 300 g doll inside the washer. The rotation period of the drum is adjustable. Find the maximum rotation period of the drum that keeps the doll stuck to the drum at its highest position.

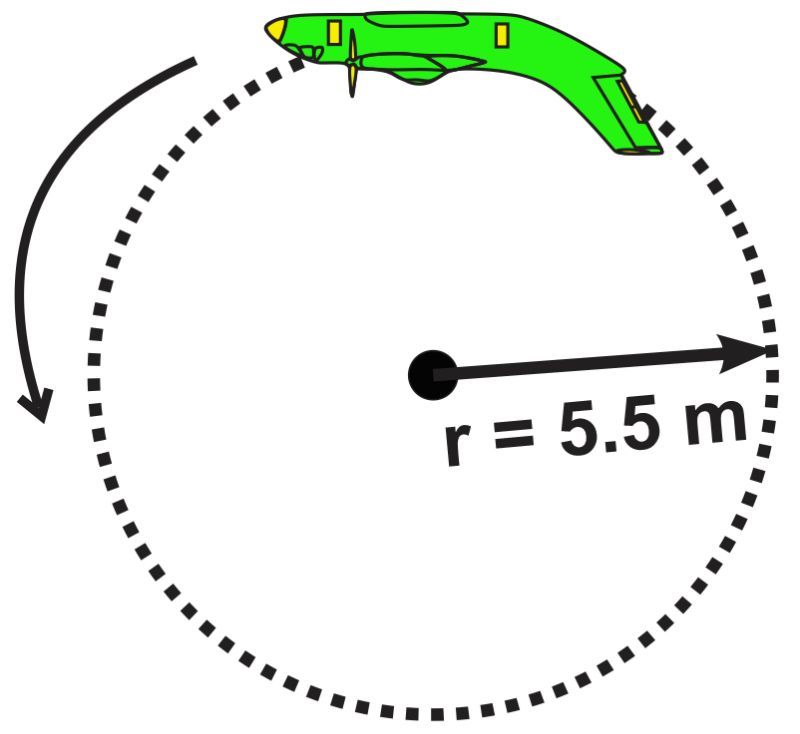
A low-flying jet plane performs a loop-the-loop in such a way that at the topmost point of the loop, the jet is upside down. Inside the jet, the pilot has forgotten to fasten her seatbelt. Given that, the radius of the loop is 5.5 m determine what the minimum speed of the jet plane should be so that the pilot does not fall out of her seat at the topmost point of the loop. 

An automobile of mass 1200 kg travels at 14 m/s around a flat curve with a radius of 50 m. What is the bare minimum coefficient of friction that the tires must have with the ground in order for the car to turn?

The banked, circular highway curves are specifically designed for high-speed driving. To prevent vehicles from slipping outward, an 85 m radius highway curve is banked at a 28° inclination. Determine the maximum speed with which a high-speed car weighing 1800 kg can safely maneuver this curve without sliding off the road. The coefficient of friction between the tire and the road is 1.