Suppose that the particle's position depends on time and it moves according to the equation x = (1/3t³ - t²)m and y = (1/4 t²-t)m. Determine where the particle is at (i) t = 0 s and (ii) t = 6 s. Also, find its speed at the given time intervals.

A hiker starts at a campsite and walks 15 km north, then turns and walks 11 km west, and finally, walks 8.0 km south. Calculate the hiker's final displacement from the campsite. Assume the distances are measured in a straight line.

At t= 0, a submarine is moving at v = -8.0 ĵ m/s and is located at r₀ = 5000 î + 125 ĵ + 750 k̂  ( in meters) with respect to a reference island. At t= 0 s, the submarine accelerates at a rate of a = 1.25  î - 2.50  ĵ (m/s²) for 2 minutes. Calculate the submarine's position vector after 2 minutes of motion.

A watermelon is rolled horizontally off the top of a bridge with an initial speed of 8.0 m/s. The watermelon travels 12 m horizontally before hitting the ground. Determine the height of the bridge.

The horizontal and vertical components of the velocity of an ice skater performing in a horizontal frictionless arena are shown in the figure below. At t = 0 s, the ice skater's initial position vector is r₀ = 0 î + 0 ĵ. Determine the direction of the velocity vector of the ice skater with respect to the positive horizontal direction at time t = 3 s.

Recently, there are reports of people throwing plastics on the waters of a local lagoon. To address this, the caretakers check the area by using drones. The velocity of a drone can be expressed as a function of time, and it is described by the equation

Find the magnitude and direction of the drone's velocity and acceleration 3 seconds after launch.

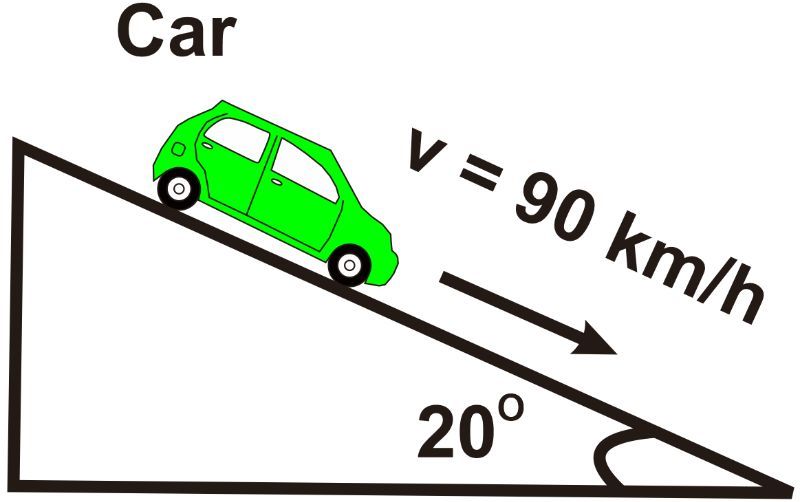
On a slope with a constant incline of 20.0°, a car descends. When the brakes are applied, the car's speed decreases from 90.0 km/h to a complete stop in 6.00 seconds. Calculate the horizontal and vertical components of the car's acceleration during this braking process.

A drone is initially at rest at the origin point, coordinates (0,1), and begins to move across the xy-plane. It accelerates at a constant rate, described by the vector $\vec{a}=(5.0\hat{i}+7.0\hat{j})\mathrm{\ m}/\mathrm{s}^2$. What is the drone's speed as a function of time?

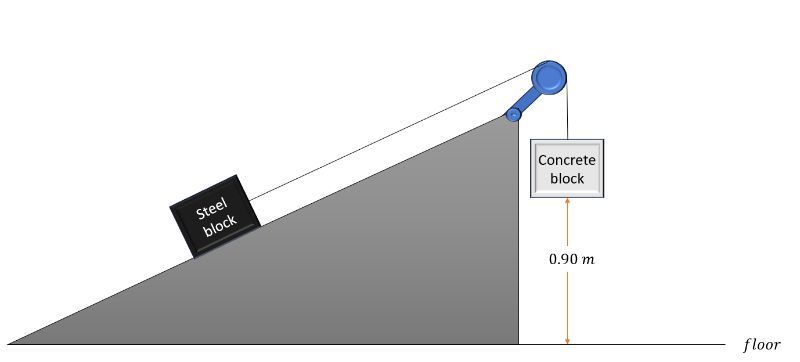
A steel block, with a mass of 4.5 kg, and a concrete block, with a mass of 5.5 kg, are positioned on a frictionless inclined plane as shown. The concrete block is initially 0.90 m above the floor. The falling concrete block causes the steel block to accelerate at 5.4 m/s² on the frictionless surface. Given that the system starts from rest and air resistance is negligible, calculate the velocity of the concrete block just before it makes contact with the floor.

Two circus artists ride two unicycles. The artist dressed in red has a velocity v_r = 1.5 î (m/s), and the one dressed in blue has a velocity v_b=-2.5 ĵ  (m/s). How fast does the artist dressed in blue appear to be moving compared to the artist dressed in red?

The pilot of a trainer plane wants to travel due east. A wind which is classified as "storm" by the weather station blows toward the north at a speed of 100 km/hr (approximately 62.1 mi/h). In what direction relative to the east-west line should the pilot travel if the airspeed of the plane (its speed in still air) is 300.0 km/h (about 186.4 mi/h)?

An athlete is practicing rowing in a river that is 50.0 m wide. The river's current flows at 0.80 m/s. The athlete can row with a speed of 2.50 m/s relative to the water. If the athlete starts from one bank and rows directly across to the other side, determine the time it takes to reach the opposite bank and the distance downstream where the athlete lands, assuming the athlete initially aims to land directly opposite the starting point as shown.