A physicist is experimenting on an elastic thread to make some observations. He fixes one end of the thread to the ceiling of his lab and attaches a block of 3.25 kg to the other end. This extends the length of the thread by 0.125 m when the block comes to a rest at the equilibrium. He then pushes the block vertically down from the equilibrium position, extending the thread further by 0.250 m. If he releases the block then, after what time does the block reach back up to the equilibrium position?

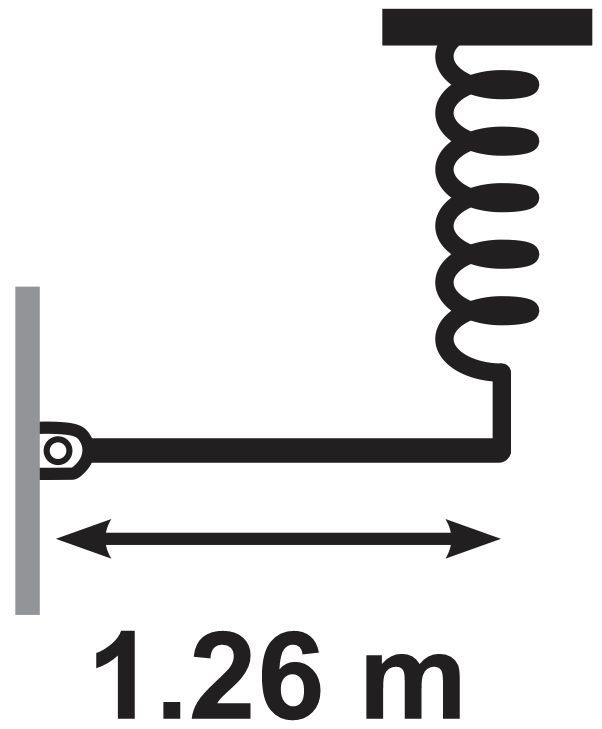
What is the oscillation frequency of a uniform rod that is 1.26 m long and has a mass M? The rod is hinged at one end and connected to a spring with a spring constant k at the other end. It is initially held horizontally and then allowed to perform small vertical oscillations. To determine the frequency, apply the torque equation about the hinge point when the oscillation is small.

You construct a 0.84 m long simple pendulum using a light string then displace it by 4.30° on one side before releasing it to oscillate. Next, you double the displacement angle to 8.60° on the same side. What is the difference between the two time periods for the two angles used?

A bob of mass 125 g is suspended from a 105 cm long massless thread. The ball is given an initial displacement of 8 degrees. Calculate the number of times the bob goes through the equilibrium position in 10.0 s.

Imagine a spherical ball named "OrbMover" suspended from a ceiling and initially hanging at a rest angle of 9.5° from the vertical. Determine the new angle that OrbMover must reach if its total potential and kinetic energy combined are to be doubled.

A fork-shaped metallic plate oscillates between the North and south poles of a magnet. Its amplitude is reduced to 42.8% of the initial amplitude in 8.60 s. Calculate the time constant.

Consider a 0.838-kg object named "OscilloBlock" attached to a spring with a spring constant of 42.0 N/m. This object moves through a medium that provides a damping force characterized by F=−bv, where b=0.665 N⋅s/m. Determine the period of OscilloBlock's motion as it undergoes damped oscillation.

An 1160-kg car, named "ShakyRide," features suspension springs with 15,000 N/m stiffness. One of the car's wheels is imbalanced due to uneven mass distribution, leading to vibrations at specific speeds. Given that the tire radius is 43 cm, determine the speed at which the wheel exhibits maximum shaking.

In a laboratory experiment, a 0.836-kg cube is set to oscillate at the end of a spring with a constant of 44.0 N/m. The cube moves in a fluid, introducing a resistive force represented by F=−bv, with b=0.672 N•s/m. If initially at t=0 the cube's displacement is x=0, and at t=2.00 s it's x=0.140 m, calculate the cube's displacement as a function of time. Use equation x=Ae^-γt sin(⁡ω' t) where ⁡ω' is the damped angular frequency and γ is the damping coefficient and equals to $\frac{b}{2m}$.