A uniform pine plank of length 2 m and a mass of 15 kg is held by a carpenter and his son. The carpenter applies a vertical force of magnitude 40 N at the left end. Find i) the magnitude and ii) the point of application of the force that the son should exert to maintain the board stable. Start by drawing a free-body diagram of the plank.

A 35 kg dog begins to cautiously tread on a 6.2 meter long, 58 kg wooden plank that is supported by two support beams. With safety in mind, determine the nearest distance the dog can approach the right end of the wooden plank without causing it to topple over.

Find the tension in the support cable angled at 36.0° and the horizontal and vertical forces that the hinge exerts on the beam at the wall, given that a cafe's outdoor sign weighing 216 N is affixed to the end of a uniform 156-N beam.

A warehouse has dimensions of 20 meters by 30 meters and a roof with a total mass of 1.5×10⁴ kg. The roof is to be supported by vertical steel columns, each with a square cross-section of 20 cm by 20 cm. These columns will be evenly distributed along the longer sides of the warehouse. Given only compression and assuming a safety factor of 8, determine the number of columns required on each longer side of the warehouse and the spacing between each column. The compression strength for steel is 2.5×10⁸ N/m².

A 180 gram steel rod that is 32 centimeters long connects a 400 gram marble to another 800 gram marble. Determine the distance between the center of mass and the 400 gram marble.

Four distinct spherical balls are connected by a glass rod (negligible mass) in the shape of a rectangle. The spherical balls are located at the vertices of the rectangle as shown in the figure. Determine the coordinates of the center of mass for this configuration.

In a stacking tournament, competitors are given three identical, uniform rectangular wooden pieces, each with a length L and mass M. Competitors stack the wooden pieces on a horizontal platform, aiming to have the top piece project as far as possible from the edge while maintaining the stack's stability. If the wooden pieces are stacked with their longest edge parallel to the platform, determine the maximum horizontal distance that the top-most wooden piece can project from the edge of the platform.

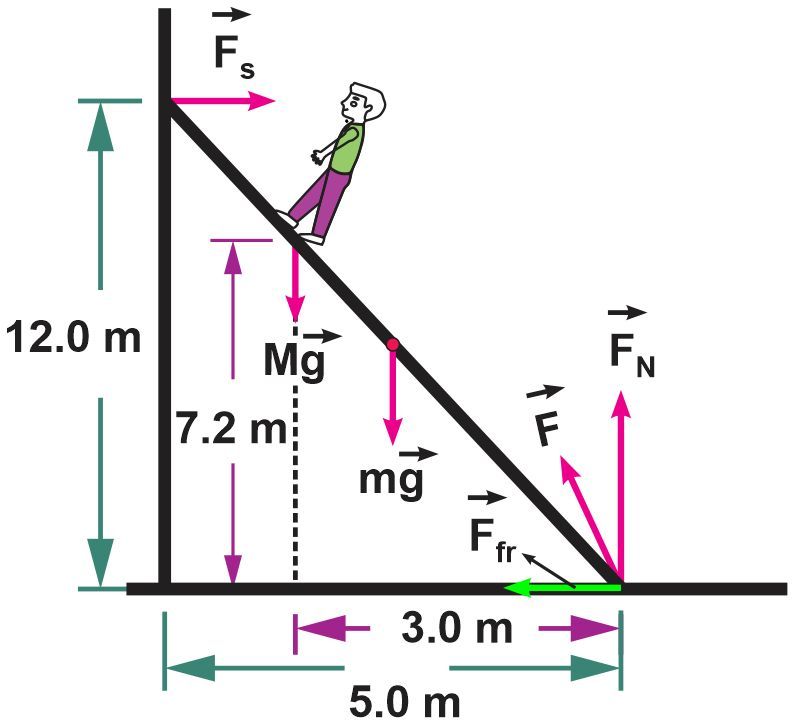
A painter places a 13 m long regular ladder against a vertical wall with negligible friction. The ladder's lower end is 5 m from the wall. Take the weight of the ladder to be 250 N and the coefficient of static friction between the floor and the ladder's foot to be 0.65. If a painter weighing 650 N climbs gently up the ladder, determine the maximum friction force that the floor can apply on the ladder's lower end.

Consider a situation where a ladder is resting on a smooth vertical surface, forming an angle with the ground. The ladder is of uniform density and has a mass of 10.0 kg. A person with a mass of 60.0 kg stands on the ladder. As the person walks towards the higher end of the ladder, it starts slipping when the person is 60% of the way from the lower end to the higher end along the length of the ladder. Determine the coefficient of static friction(μ) between the ladder and the ground.