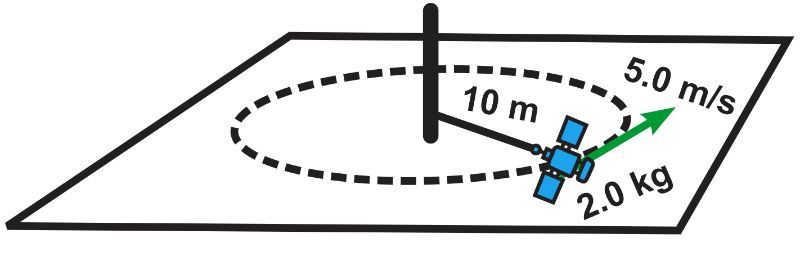
In a simulation of orbital mechanics, a model space station module of mass 2.0 kg is tethered to a central pivot by a strong, lightweight cable 10 m long. Initially, the module orbits the pivot in a horizontal plane at a speed of 5.0 m/s. To simulate a maneuver to a higher orbit speed for docking purposes, the cable is gradually pulled in, reducing the orbit's radius to 6.0 m. Determine the work done to achieve this higher orbit speed.

A ring with an inner radius of 2.0 cm and an external radius of 5.0 cm is released on an inclined surface, making an angle of 25° with the horizontal. The ring rolls over the 1.0 m long incline. i) Find the speed at the end of the incline. The ring is replaced with a sliding object. ii) Find the ratio (r) of the speed of the sliding object to the rolling ring at the end of the incline. Assume the incline is frictionless.

Consider a bowling ball of radius r that rolls without slipping inside a semispherical bowl of radius R, where R is greater than r. The bowling ball starts from rest at a point level with the rim of the bowl. Determine the speed v of the bowling ball when it reaches the bottom of the bowl, assuming no energy is lost to friction.

A mechanic is examining a tire. The moment of inertia about its spindle is given by 1/2 mR². He hoists the tire up, sets it with an angular velocity of ω_i, and brings it back to the ground. Right at the moment when the tire makes contact with the ground, the center of mass of the tire has a velocity of zero. After touching the ground, the tire initially skids on it, and then travels forward and in the end starts to roll without skidding. Determine the direction in which the friction force acted on the skidding tire.

A Physics professor is experimenting with a solid cylinder attached to a rod that passes through the center of mass of the cylinder and is perpendicular to its flat surfaces. She holds the cylinder by the rod in the air and sets it with angular speed ω_i. Afterward, she lowers it onto the ground. Just when the cylinder's surface touches the ground, the speed of the center of mass of the cylinder is zero. Though in the beginning, the cylinder skids on the ground eventually it rolls without skidding. Given that the moment of inertia of the solid cylinder about the rod is I = 1/2 mR², and the coefficient of friction between the cylinder and the ground is μ, determine for how long the cylinder skids on the ground before it rolls without skidding.

[Hint: Apply ∑F = ma, ∑τ_cm = I_cmα_cm, and consider that v_cm = ωr only when the cylinder rolls without skidding.]

A metal piece of mass M is extended to form a planar rectangular sheet. If the length of the sheet L is twice the width, find the moment of inertia about an axis perpendicular to the sheet and passing through one of the four corners.

A cylinder of mass M, radius R, and length L is tightly fitted with an axle that acts like a rotational axis at a distance (3/5)R from the center of the cylinder. The axle has a radius r. A thread wound on the axle is pulled with a tension T. Assuming the axle to have an insignificant moment of inertia, derive an expression for the cylinder's angular acceleration.

A child's entertainment equipment has a 100.0 cm long, thin and uniform rod of mass 0.500 kg. Determine the moment of inertia of the rod pivoted about its center such that it spins perpendicular to its length. 

A uniform square slab of side a and mass m_s placed in the horizontal plane revolves around a vertical axis passing through its center. Write the expression of the moment of inertia.

A rectangle houses four masses, as shown below. The masses are linked using rods of negligible mass. Calculate the system's moment of inertia about an axis (diagonal) through masses 1 and 3.

A 10 kg rectangular wooden plank with dimensions 180 cm by 40 cm is used as a seesaw. What is the moment of inertia of the plank when it rotates about its centre of mass?