The impact resistance of new motorcycle helmets is tested by striking them against rigid barriers at a speed of 20 m/s. A prototype helmet, weighing 2 kg, comes to a complete stop in 0.2 seconds upon impact. Determine the average force exerted on the helmet by the barrier during the collision.

Calculate the vertical and horizontal components of the pendulum’s maximum displacement when a 29-g steel ball launched at 211 m/s embeds itself in a 3.5-kg pendulum hanging from a 2.9-m-long wire, causing the pendulum to swing upward in an arc.

A group of physics students is conducting an experiment using an air track. They have a 35 cm long massless spring with a spring constant of 10 N/m attached to the track at one end and an air track car of mass 320 g at the other end. The air track car is initially at rest. The students launch a second air track car of mass 600 g, towards the first. When the second air track car collides with the first, it sticks to it, causing the spring to compress by a distance of 20.0 cm from its natural length. Determine the velocity of the 600 g air track car right before the collision.

A piece of cardboard is kept perpendicularly on a horizontal surface by attaching it to one end of a spring. The other end of the spring is attached to the wall. An arrow of mass M = 0.021 kg is shot at the cardboard target. As a result, it gets attached to the cardboard and compresses the attached spring by a distance s = 0.060 m before stopping. Given that the coefficient of kinetic friction between the cardboard and the horizontal surface is μ_k = 0.30, the spring constant is k = 120 N/m and the piece of cardboard has a mass m = 0.788 kg, calculate the fraction of the initial kinetic energy of the arrow that is lost during the collision between the arrow and the cardboard, considering only the immediate aftermath of the collision, without considering other dissipative effects.

A toy car that has a mass of 𝑚 = 0.30 kg is rolling on a smooth tile floor when it crashes into a stationary toolbox that has a mass of 𝑀 = 2.70 kg. The toy car embeds itself into the toolbox, causing it to slide across the floor. The toolbox compresses a spring, that has a spring constant of 𝑘 = 200 N/m, by a distance of 𝑥 = 0.10 m before coming to rest. The coefficient of kinetic friction between the toolbox and the floor is 𝜇_k = 0.30. Determine the initial speed of the toy car just before the crash. Hint use 𝑔 = 9.8 m/s² .

Two cars collide with each other. Car A has a mass of 1000 kg and is moving towards car B with a velocity of 20 m/s. Car B has a mass of 800 kg and is at rest. What is the velocity of each car immediately after they collide?

We assume this is a one-dimensional collision that obeys the conservation laws of momentum and
mechanical energy.

The image below shows the momenta of toys A and B before the collision, as well as the momentum of toy B after the collision. The toys separate after the collision. Determine the momentum of toy A after the collision, giving the result in unit vectors.

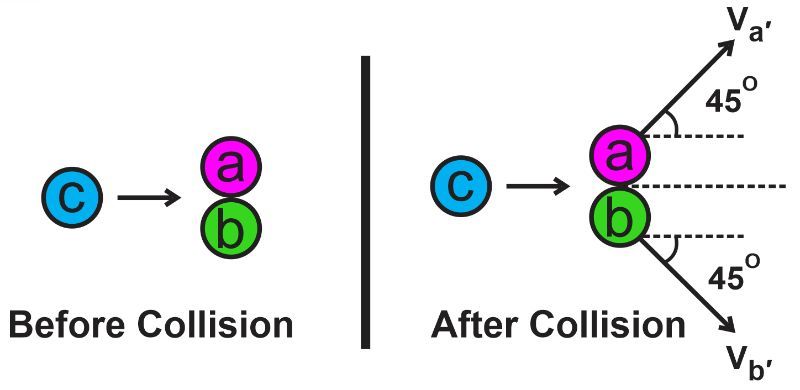
Two identical marbles on a frictionless surface are initially at rest. They are then struck by a third identical marble moving horizontally at 1.5 m/s as shown in the figure below. After the collision, both of the first two marbles move at an angle of 45° to the initial path of the third marble. Assuming the collision is perfectly elastic, find the speeds of all three marbles post-collision.

On a nearly frictionless ice surface, a 53-kg skater and a 73-kg hockey player stand 10.1 m apart. Calculate how far from the skater their center of mass is.

Calculate the center of mass of a phosphine molecule (PH₃) relative to the center of its base. The molecule consists of a phosphorus atom at the apex of a pyramid and three hydrogen atoms at the corners of an equilateral triangle that forms the base. The side of the triangle is 0.14 nm, and the vertical distance from the phosphorus atom to the plane of hydrogen atoms is 0.10 nm.

A research balloon, equipped for atmospheric studies, is stationary at a high altitude above the Earth's surface. It has a total mass $M_1$ , including both the balloon and attached scientific instruments. For specific data collection, one instrument package, with a mass $M_2$ , needs to be lowered to a different altitude. This instrument package is allowed to slide down a rope at a speed v relative to the balloon. Calculate the velocity $V_b$ of the balloon relative to the Earth immediately after the package starts sliding. What happens to the balloon's velocity relative to the Earth if the instrument stops sliding?