A 5-g ping pong is fired straight up using the elastic energy that has been stored in the rubber band of a slingshot. At a height of 10 meters above the release position, the speed of the ball is zero. How much potential energy is contained in the rubber band?

Understanding the potential energy changes along the path can provide valuable insights into the energy state of the system. Suppose a one-dimensional system (m = 400 g) is being acted upon by a conservative force F_x, with the potential energy set to zero at a reference point x = x₀. Calculate the system's potential energy at various points along the path: (i) x = x₀ + 2.0 m, (ii) x = x₀ + 4.0 m, (iii) x = x₀ + 6.0 m, and (iv) x = x₀ + 8.0 m, where x₀ = 0 m.

A stream of electrons causes an emission at λ = 122 nm on He ⁺ ions due to the transition from the 4^th to 2^nd energy level. Determine the electric potential used to accelerate the electrons. Assume He⁺ ions do not gain additional electrons in the process.

If the center of mass of a 59-kg pole jumper rises 5.0 m during the jump, what is the change in gravitational potential energy?

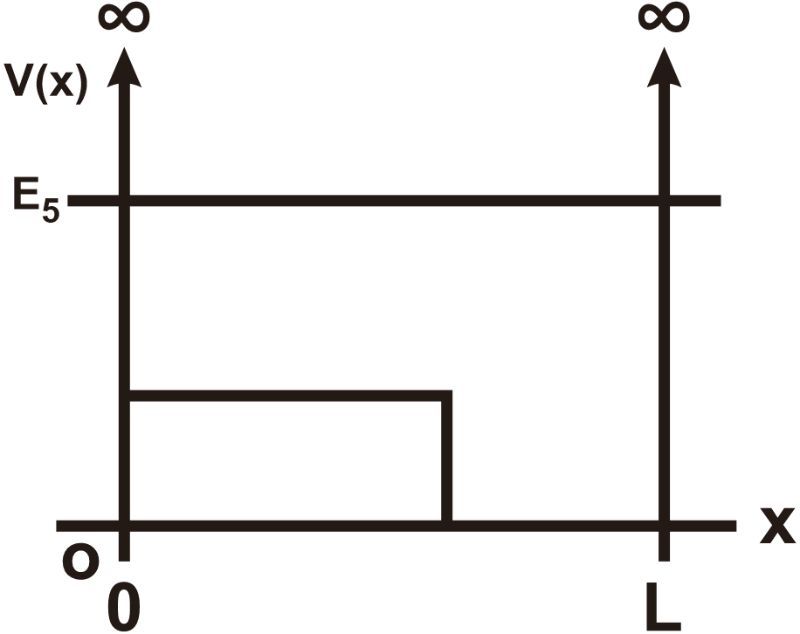
Draw the wave function corresponding to n=5 for the potential energy depicted in the figure below.

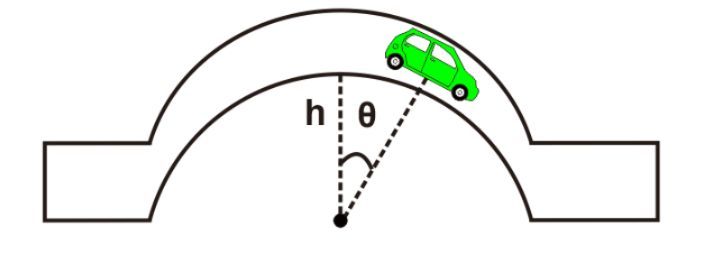
A driver starts his car resting on top of a semicircular hill. The road leading to the foothills is frictionless and curved. Derive an equation to calculate the car's speed at an angle θ as depicted in the figure below.

A science teacher pushes a 0.75 kg cube against an ideal spring with a spring constant of 300 N/m. The spring is compressed to a distance of 5.0 cm. The teacher releases the cube. After moving over the smooth horizontal part of the setup shown in the figure below, the cube slides down over a rough ramp, making an angle of 15° with the horizontal. The coefficient of kinetic friction between the cube and ramp is 0.25. Determine the speed of the cube just after leaving contact with the spring.

A block placed at the top of a ball of radius R slides down its surface from rest. In the presence of friction, does the block fly off at a greater angle than if there is no friction? Assume that the mass of the block is M.

You obtain a massless spring from an old umbrella having a force constant, k = 1000 N/m. Out of sheer fun, you place the spring to rest vertically with one of its ends lying on a bench. Next, you release a block of mass 0.50 kg from a height of 1.5 m (measured from the spring's top end) directly above the spring. Determine the maximum compression that occurs on the spring.

A 25 kg crate is released from up an incline that makes 50° with the horizontal, such that it slides a distance of 3.5 m before striking a spring. The force constant of the spring is 320 N/m. Calculate the greatest compression that occurs on the spring.

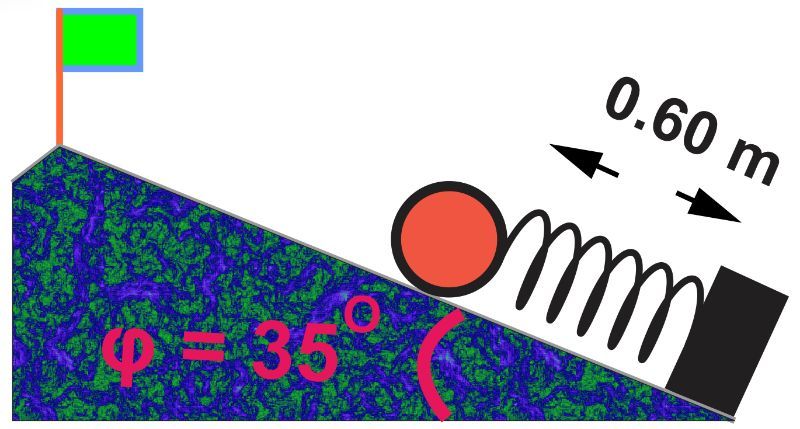
A bowling ball of mass 5.0 kg is kept at the free end of a compressed spring (k = 62 N/m) installed at the bottom of a steep hill. The hill makes an angle of 35° with the horizontal at the bottom of the hill. Given that, the equilibrium length of the spring is 1.50 m and the compressed spring length is 0.60 m calculate how far up the hill the bowling ball will travel before coming to a stop if the spring is released. (Assume that friction is negligible.)

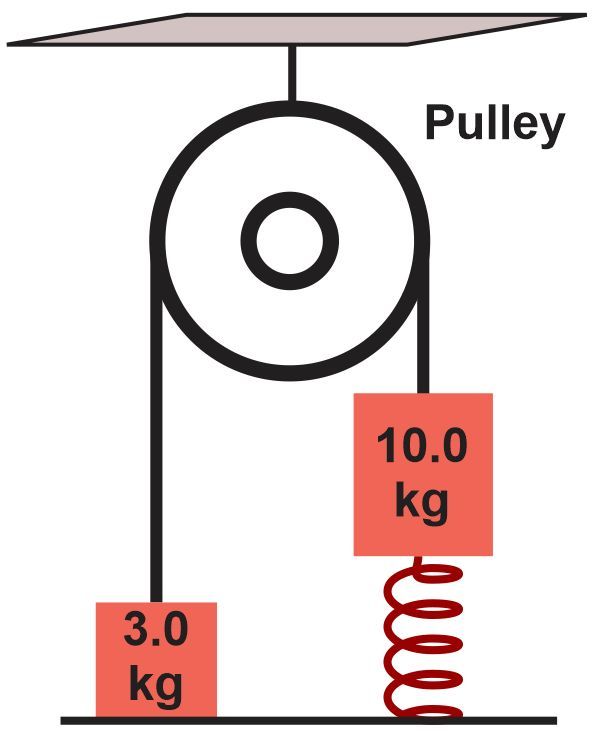
In a storage room, a heavy box of mass $10.0$ kg is initially at rest on a spring with a spring constant of $800$ N/m. The box is part of a pulley system where it is connected to a $3.0$-kg package. When the system is released, the heavier box compresses the spring by moving downwards, pulling the lighter package upwards. Calculate the distance the box falls, compressing the spring, before the entire system momentarily comes to rest.

The binding energy of the single electron in He⁺ is 24.6 eV and the mass of He⁺ is 4.001506 amu. Calculate the percentage decrease in mass when a He²⁺ ion gains an electron to form the He⁺ ion. Express the result in amu and as a percentage of He ²⁺ mass.

Use the conservation of energy principle to calculate the minimum speed required for the object to travel from point B to point A if the mass of the object is 120g.

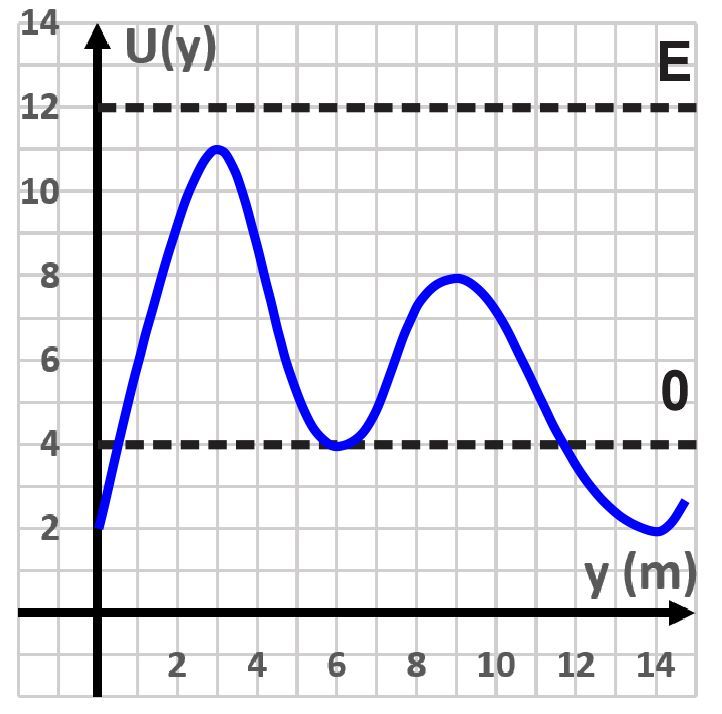
A conservative force acts on a ball along the y-axis. As a result, it moves along the same axis. Its potential energy versus the y-axis graph is given below. It can be seen that the total energy E > U(y), which implies the speed of the ball is always non-zero. Find the interval(s) of y in which the force on the ball acts toward the positive y direction.