Express the following measurement in complete decimal form, without using any unit prefixes: 9.8 µm

The position of a free falling object at any instant is given by the equation: y = ½ gt², where y and t have units of meter and seconds, respectively. Determine the unit of constant 'g'.

When manufacturing precision-engineered components for a spacecraft, the length of a critical component needs to be determined with extreme accuracy. If this component should have a length of 30 cm to within ±0.1 mm, what percentage of uncertainty in the length is permissible, and how many significant figures should be used in the measurement of the length?

The Recommended Dose Allowance (RDA) for the trace metal lead through diet is 0.000114 g/day, based on allowable lead intake for adults. Express this dose in microgram per day.

While riding an electric motorcycle, it has a top speed of 75000 furlongs per fortnight. How many miles per hour is this? Round up to the nearest whole number.

A large water tank that is used for storing rainwater has a cylindrical shape with a diameter (d) of 3.00 m and a height (h) of 5.00 m. What would be the dimensions of the water tank expressed in feet for the diameter (d) and height (h), and what would be the estimated volume (V) of the water tank expressed in cubic feet?

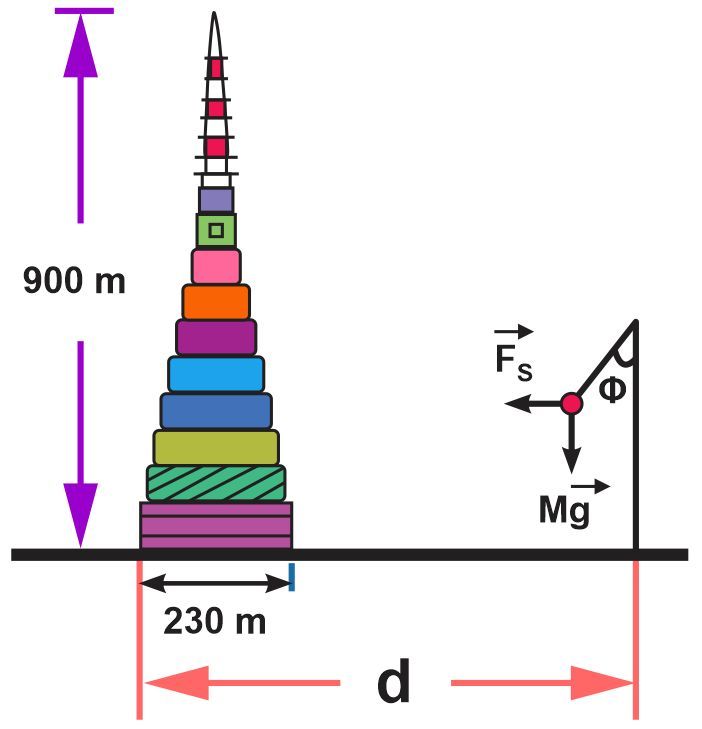
A student comes up with a clever way of calculating the mass of a 900 m tall skyscraper found standing alone in the middle of a desert. He places a pendulum near it. The mass of the bob of the pendulum is M and it makes an angle of Φ with the vertical because of the gravitational attraction created by the skyscraper. To compare his calculations made with the pendulum, he first estimates the mass conventionally. To simplify his calculations, he treats the skyscraper like a cone with the diameter of the base being 230 m. He takes the density of the building to be 19 kg/m³, in order to help him complete his computations. Assuming that he makes no errors, what is his estimation of what the mass value will be?

Astronomers are always on the lookout for objects that can potentially be hazardous if they crash into our planet. In the past, they spotted one such object having a strange dimension of 20 km × 10 km × 7 km. A space probe was sent to study the object that orbited it at an altitude of 5 km above its surface. They estimated its density to be 5.6 × 10³ kg/m³. For comparison, determine the radius of a spherical asteroid having the same mass and density.

The following relation represents a physical quantity called drag force, F = Cρ^αv^βA^γ where α, β, γ, and C are dimensionless quantities. ρ is the density of fluid, v is the velocity and A is the cross-sectional area. Using dimensional analysis, determine the formula of drag force.

What should be the dimensions of the quantity R formed by the following combination: R = √[(hc)/G] where G (gravitational constant), h (Planck's constant), and c (speed of light) are three universal constants.

Determine the number of gallons of diesel used in Arizona in one day. The average mileage of a car is approximately 30 miles per gallon, and each car is driven an average of 12,000 miles annually. There are four cars for every five people and there is an estimated 7 × 10⁶ people in the state of Arizona. Answer in three significant figures.

Determine the number of significant figures in 50047

Following the rules of significant figures simplify the expression 21.8/16.9

What is the largest angle θ, rounded to two significant figures, for which the numerical values of cos θ and cot θ are approximately equal?