Here are the essential concepts you must grasp in order to answer the question correctly.
Vector Cross Product
The vector cross product is a mathematical operation that takes two vectors and produces a third vector that is perpendicular to the plane formed by the original vectors. The direction of the resulting vector is determined by the right-hand rule, and its magnitude is equal to the area of the parallelogram formed by the two vectors. This operation is fundamental in physics for calculating torque, angular momentum, and magnetic force.
Recommended video:
Vector (Cross) Product and the Right-Hand-Rule
Unit Vectors
Unit vectors are vectors with a magnitude of one, used to indicate direction. In three-dimensional space, the standard unit vectors are î, ĵ, and k̂, which represent the x, y, and z axes, respectively. They are essential for expressing other vectors in terms of their components along these axes, simplifying vector calculations and operations such as the cross product.
Recommended video:
Right-Hand Rule
The right-hand rule is a mnemonic used to determine the direction of the resultant vector in a cross product operation. By aligning the fingers of the right hand along the first vector and curling them towards the second vector, the thumb points in the direction of the resulting vector. This rule is crucial for visualizing and understanding the orientation of vectors in three-dimensional space.
Recommended video:
Force on Moving Charges & Right Hand Rule
 Verified step by step guidance
Verified step by step guidance Verified Solution
Verified Solution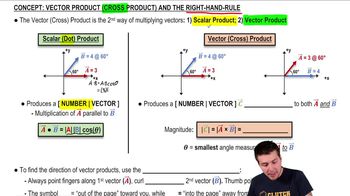



 1:30m
1:30m