Here are the essential concepts you must grasp in order to answer the question correctly.
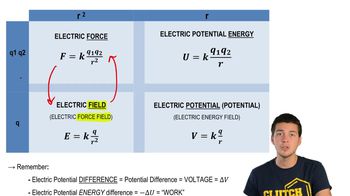
Electric Potential
Electric potential, denoted as V, is the work done per unit charge in bringing a positive test charge from infinity to a point in an electric field. It is a scalar quantity and can be calculated for different regions in a system of charges. In this problem, the potential is influenced by both the inner sphere and the outer shell, and the total potential is the sum of the potentials due to each charge distribution.
Recommended video:
Gauss's Law
Gauss's Law relates the electric field through a closed surface to the charge enclosed by that surface. It is particularly useful for calculating electric fields in symmetric charge distributions, such as spherical shells. In this scenario, Gauss's Law helps determine the electric field both inside and outside the spherical shell, allowing for the derivation of the electric field expressions needed for the problem.
Recommended video:
Electric Field and Potential Relationship
The electric field (E) is related to the electric potential (V) by the negative gradient of the potential, expressed as E = -∂V/∂r. This relationship indicates how the electric field can be derived from the potential function. In this question, understanding this relationship is crucial for calculating the electric field in different regions between and outside the spheres, as well as for deriving the expressions for parts (c) and (d).
Recommended video:
Relationships Between Force, Field, Energy, Potential