All right, guys. So in these videos, I'm going to teach you how to use free energy in kilojoules per mole to calculate the exact percentages of each conformation that you would get of a cyclohexane. Again, these videos might be beyond the scope of what your professor wants you to know for your test. So I'm going to leave it up to you to if you need to know this or not. You've been warned, so it's time to get into this. It turns out that we can use that delta G value that we get from our A values to calculate those exact percentages at any given temperature. Now the way we do this is through the Gibbs free energy equilibrium constant equation. Just so you guys know, if this equation looks familiar, it's not unique to this type of problem. In fact, pretty much any process that you can describe a free energy difference in can, you can determine an equilibrium through this equation. So this is a very important equation for all of chemistry, not just for cyclohexanes. Okay? Now as you can see, what it says is that let's just go through one term at a time. It says that the delta G for the change in free energy is equal to the negative R. Now remember that R is the gas constant that we used to use in general chemistry and there were 2 different values of R that we used to use. Just note that the one we're using is in joules per mole, so that's 8.134. That's going to be important in a second. Then temperature, temperatures in Kelvin. Remember that I mean it's been a while since we dealt with temperature, but remember that 0 degrees Celsius is equal to 273.15 degrees Kelvin. That's going to be a conversion that we have to use in a little bit. Then you're going to multiply that by the natural log of the equilibrium constant. Well, in order to solve any of these problems for percentages, we need to know the value of the equilibrium constant. Because equilibrium constant by definition tells you what's your products over your reactants. I need to know that fraction. If we go ahead and we solve for KE, I did the math for you. Don't worry. What we get is that the KE is equal to the negative delta G over the R times the T, all to the e. If we can just plug in these variables, we're going to get the equilibrium constant. Now we know what R is. We know what T is. Your calculator tells you what E is. All we need is negative delta G. Do we have a way to find that? Yes, guys. That's through our A values. Our A values tell us what the free energy changes as we go axial. Awesome. Now I do want to make one note of the delta G. Notice that this is negative delta G. But everything that we solved when we're doing A values, we were actually solving for positive delta G because we were actually looking at the less stable one. We're looking at how much energy do we have to put into the system to go to axial. When we use this equation, we're actually going to be inputting the positive delta G here and that's fine. What we're going to be getting is a number that describes basically how we're going to that less stable value. So then over here, what we have is that then we get that KE and now we can solve for the percentages using the definition, products over reactants. Once we get that positive KE number, that positive KE number means that we're actually going towards the favored direction. I'm not sure if you guys remember but if you have a KE over 1, that means you're going to the more favored direction. I'm just telling you guys right now, if we use a positive number for delta G, we're going to get also a positive number. I'm sorry. We're going to get a number that's above 1 for KE. We're going to get this greater than 1. What that means is that our definition of KE has to be the products over the reactants, meaning the more favored conformation over the less favored. Just letting us know that the way that we've arranged this equation, the way that your textbook does it, is that it always does the more favored over the less favored. Meaning that when you get this positive value, it's going to tell you what percentage you're going to have of the equatorial. And then that minus 100 will be your axial. Now here it says that KE is equal to X over one over X. That just has to do with the definition of equilibrium constant. How KE is what your X is what you're making. That's your product. So then one minus whatever you made would be your reactants. Then we don't really want KE here. We want X because we're really trying to figure out how much of this product we're going to get. So if we solve for X, I did that for you. What you're finally going to get is that X is equal to KE over KE+1. If you want to put it in a percentage term, it's times 100. Now that was a ton of words that I just said, a lot of numbers and symbols. I do not need you guys to perfectly understand this as much as I just need you to memorize it and know how to use it. If your professor wants you to solve this on your exam, then these equations should be in your mind. You should have memorized this equation. You should have memorized the definition of KE or how to solve for X. Now we're going to focus on the actual working part, on the actual part that we determine percentages which is so cool. I'm a huge Orgo nerd as you guys know. This is fun. Getting to determine the exact percentage of each cyclohexane. This first one will be a worked example and we'll go ahead and start off with this first one. I'm just going to pause the video and then we'll come back and we'll solve this one together.
- 1. A Review of General Chemistry5h 5m
- Summary23m
- Intro to Organic Chemistry5m
- Atomic Structure16m
- Wave Function9m
- Molecular Orbitals17m
- Sigma and Pi Bonds9m
- Octet Rule12m
- Bonding Preferences12m
- Formal Charges6m
- Skeletal Structure14m
- Lewis Structure20m
- Condensed Structural Formula15m
- Degrees of Unsaturation15m
- Constitutional Isomers14m
- Resonance Structures46m
- Hybridization23m
- Molecular Geometry16m
- Electronegativity22m
- 2. Molecular Representations1h 14m
- 3. Acids and Bases2h 46m
- 4. Alkanes and Cycloalkanes4h 19m
- IUPAC Naming29m
- Alkyl Groups13m
- Naming Cycloalkanes10m
- Naming Bicyclic Compounds10m
- Naming Alkyl Halides7m
- Naming Alkenes3m
- Naming Alcohols8m
- Naming Amines15m
- Cis vs Trans21m
- Conformational Isomers13m
- Newman Projections14m
- Drawing Newman Projections16m
- Barrier To Rotation7m
- Ring Strain8m
- Axial vs Equatorial7m
- Cis vs Trans Conformations4m
- Equatorial Preference14m
- Chair Flip9m
- Calculating Energy Difference Between Chair Conformations17m
- A-Values17m
- Decalin7m
- 5. Chirality3h 39m
- Constitutional Isomers vs. Stereoisomers9m
- Chirality12m
- Test 1:Plane of Symmetry7m
- Test 2:Stereocenter Test17m
- R and S Configuration43m
- Enantiomers vs. Diastereomers13m
- Atropisomers9m
- Meso Compound12m
- Test 3:Disubstituted Cycloalkanes13m
- What is the Relationship Between Isomers?16m
- Fischer Projection10m
- R and S of Fischer Projections7m
- Optical Activity5m
- Enantiomeric Excess20m
- Calculations with Enantiomeric Percentages11m
- Non-Carbon Chiral Centers8m
- 6. Thermodynamics and Kinetics1h 22m
- 7. Substitution Reactions1h 48m
- 8. Elimination Reactions2h 30m
- 9. Alkenes and Alkynes2h 9m
- 10. Addition Reactions3h 18m
- Addition Reaction6m
- Markovnikov5m
- Hydrohalogenation6m
- Acid-Catalyzed Hydration17m
- Oxymercuration15m
- Hydroboration26m
- Hydrogenation6m
- Halogenation6m
- Halohydrin12m
- Carbene12m
- Epoxidation8m
- Epoxide Reactions9m
- Dihydroxylation8m
- Ozonolysis7m
- Ozonolysis Full Mechanism24m
- Oxidative Cleavage3m
- Alkyne Oxidative Cleavage6m
- Alkyne Hydrohalogenation3m
- Alkyne Halogenation2m
- Alkyne Hydration6m
- Alkyne Hydroboration2m
- 11. Radical Reactions1h 58m
- 12. Alcohols, Ethers, Epoxides and Thiols2h 42m
- Alcohol Nomenclature4m
- Naming Ethers6m
- Naming Epoxides18m
- Naming Thiols11m
- Alcohol Synthesis7m
- Leaving Group Conversions - Using HX11m
- Leaving Group Conversions - SOCl2 and PBr313m
- Leaving Group Conversions - Sulfonyl Chlorides7m
- Leaving Group Conversions Summary4m
- Williamson Ether Synthesis3m
- Making Ethers - Alkoxymercuration4m
- Making Ethers - Alcohol Condensation4m
- Making Ethers - Acid-Catalyzed Alkoxylation4m
- Making Ethers - Cumulative Practice10m
- Ether Cleavage8m
- Alcohol Protecting Groups3m
- t-Butyl Ether Protecting Groups5m
- Silyl Ether Protecting Groups10m
- Sharpless Epoxidation9m
- Thiol Reactions6m
- Sulfide Oxidation4m
- 13. Alcohols and Carbonyl Compounds2h 17m
- 14. Synthetic Techniques1h 26m
- 15. Analytical Techniques:IR, NMR, Mass Spect7h 3m
- Purpose of Analytical Techniques5m
- Infrared Spectroscopy16m
- Infrared Spectroscopy Table31m
- IR Spect:Drawing Spectra40m
- IR Spect:Extra Practice26m
- NMR Spectroscopy10m
- 1H NMR:Number of Signals26m
- 1H NMR:Q-Test26m
- 1H NMR:E/Z Diastereoisomerism8m
- H NMR Table24m
- 1H NMR:Spin-Splitting (N + 1) Rule22m
- 1H NMR:Spin-Splitting Simple Tree Diagrams11m
- 1H NMR:Spin-Splitting Complex Tree Diagrams12m
- 1H NMR:Spin-Splitting Patterns8m
- NMR Integration18m
- NMR Practice14m
- Carbon NMR4m
- Structure Determination without Mass Spect47m
- Mass Spectrometry12m
- Mass Spect:Fragmentation28m
- Mass Spect:Isotopes27m
- 16. Conjugated Systems6h 13m
- Conjugation Chemistry13m
- Stability of Conjugated Intermediates4m
- Allylic Halogenation12m
- Reactions at the Allylic Position39m
- Conjugated Hydrohalogenation (1,2 vs 1,4 addition)26m
- Diels-Alder Reaction9m
- Diels-Alder Forming Bridged Products11m
- Diels-Alder Retrosynthesis8m
- Molecular Orbital Theory9m
- Drawing Atomic Orbitals6m
- Drawing Molecular Orbitals17m
- HOMO LUMO4m
- Orbital Diagram:3-atoms- Allylic Ions13m
- Orbital Diagram:4-atoms- 1,3-butadiene11m
- Orbital Diagram:5-atoms- Allylic Ions10m
- Orbital Diagram:6-atoms- 1,3,5-hexatriene13m
- Orbital Diagram:Excited States4m
- Pericyclic Reaction10m
- Thermal Cycloaddition Reactions26m
- Photochemical Cycloaddition Reactions26m
- Thermal Electrocyclic Reactions14m
- Photochemical Electrocyclic Reactions10m
- Cumulative Electrocyclic Problems25m
- Sigmatropic Rearrangement17m
- Cope Rearrangement9m
- Claisen Rearrangement15m
- 17. Ultraviolet Spectroscopy51m
- 18. Aromaticity2h 34m
- 19. Reactions of Aromatics: EAS and Beyond5h 1m
- Electrophilic Aromatic Substitution9m
- Benzene Reactions11m
- EAS:Halogenation Mechanism6m
- EAS:Nitration Mechanism9m
- EAS:Friedel-Crafts Alkylation Mechanism6m
- EAS:Friedel-Crafts Acylation Mechanism5m
- EAS:Any Carbocation Mechanism7m
- Electron Withdrawing Groups22m
- EAS:Ortho vs. Para Positions4m
- Acylation of Aniline9m
- Limitations of Friedel-Crafts Alkyation19m
- Advantages of Friedel-Crafts Acylation6m
- Blocking Groups - Sulfonic Acid12m
- EAS:Synergistic and Competitive Groups13m
- Side-Chain Halogenation6m
- Side-Chain Oxidation4m
- Reactions at Benzylic Positions31m
- Birch Reduction10m
- EAS:Sequence Groups4m
- EAS:Retrosynthesis29m
- Diazo Replacement Reactions6m
- Diazo Sequence Groups5m
- Diazo Retrosynthesis13m
- Nucleophilic Aromatic Substitution28m
- Benzyne16m
- 20. Phenols55m
- 21. Aldehydes and Ketones: Nucleophilic Addition4h 56m
- Naming Aldehydes8m
- Naming Ketones7m
- Oxidizing and Reducing Agents9m
- Oxidation of Alcohols28m
- Ozonolysis7m
- DIBAL5m
- Alkyne Hydration9m
- Nucleophilic Addition8m
- Cyanohydrin11m
- Organometallics on Ketones19m
- Overview of Nucleophilic Addition of Solvents13m
- Hydrates6m
- Hemiacetal9m
- Acetal12m
- Acetal Protecting Group16m
- Thioacetal6m
- Imine vs Enamine15m
- Addition of Amine Derivatives5m
- Wolff Kishner Reduction7m
- Baeyer-Villiger Oxidation39m
- Acid Chloride to Ketone7m
- Nitrile to Ketone9m
- Wittig Reaction18m
- Ketone and Aldehyde Synthesis Reactions14m
- 22. Carboxylic Acid Derivatives: NAS2h 51m
- Carboxylic Acid Derivatives7m
- Naming Carboxylic Acids9m
- Diacid Nomenclature6m
- Naming Esters5m
- Naming Nitriles3m
- Acid Chloride Nomenclature5m
- Naming Anhydrides7m
- Naming Amides5m
- Nucleophilic Acyl Substitution18m
- Carboxylic Acid to Acid Chloride6m
- Fischer Esterification5m
- Acid-Catalyzed Ester Hydrolysis4m
- Saponification3m
- Transesterification5m
- Lactones, Lactams and Cyclization Reactions10m
- Carboxylation5m
- Decarboxylation Mechanism14m
- Review of Nitriles46m
- 23. The Chemistry of Thioesters, Phophate Ester and Phosphate Anhydrides1h 10m
- 24. Enolate Chemistry: Reactions at the Alpha-Carbon1h 53m
- Tautomerization9m
- Tautomers of Dicarbonyl Compounds6m
- Enolate4m
- Acid-Catalyzed Alpha-Halogentation4m
- Base-Catalyzed Alpha-Halogentation3m
- Haloform Reaction8m
- Hell-Volhard-Zelinski Reaction3m
- Overview of Alpha-Alkylations and Acylations5m
- Enolate Alkylation and Acylation12m
- Enamine Alkylation and Acylation16m
- Beta-Dicarbonyl Synthesis Pathway7m
- Acetoacetic Ester Synthesis13m
- Malonic Ester Synthesis15m
- 25. Condensation Chemistry2h 9m
- 26. Amines1h 43m
- 27. Heterocycles2h 0m
- Nomenclature of Heterocycles15m
- Acid-Base Properties of Nitrogen Heterocycles10m
- Reactions of Pyrrole, Furan, and Thiophene13m
- Directing Effects in Substituted Pyrroles, Furans, and Thiophenes16m
- Addition Reactions of Furan8m
- EAS Reactions of Pyridine17m
- SNAr Reactions of Pyridine18m
- Side-Chain Reactions of Substituted Pyridines20m
- 28. Carbohydrates5h 53m
- Monosaccharide20m
- Monosaccharides - D and L Isomerism9m
- Monosaccharides - Drawing Fischer Projections18m
- Monosaccharides - Common Structures6m
- Monosaccharides - Forming Cyclic Hemiacetals12m
- Monosaccharides - Cyclization18m
- Monosaccharides - Haworth Projections13m
- Mutarotation11m
- Epimerization9m
- Monosaccharides - Aldose-Ketose Rearrangement8m
- Monosaccharides - Alkylation10m
- Monosaccharides - Acylation7m
- Glycoside6m
- Monosaccharides - N-Glycosides18m
- Monosaccharides - Reduction (Alditols)12m
- Monosaccharides - Weak Oxidation (Aldonic Acid)7m
- Reducing Sugars23m
- Monosaccharides - Strong Oxidation (Aldaric Acid)11m
- Monosaccharides - Oxidative Cleavage27m
- Monosaccharides - Osazones10m
- Monosaccharides - Kiliani-Fischer23m
- Monosaccharides - Wohl Degradation12m
- Monosaccharides - Ruff Degradation12m
- Disaccharide30m
- Polysaccharide11m
- 29. Amino Acids3h 20m
- Proteins and Amino Acids19m
- L and D Amino Acids14m
- Polar Amino Acids14m
- Amino Acid Chart18m
- Acid-Base Properties of Amino Acids33m
- Isoelectric Point14m
- Amino Acid Synthesis: HVZ Method12m
- Synthesis of Amino Acids: Acetamidomalonic Ester Synthesis16m
- Synthesis of Amino Acids: N-Phthalimidomalonic Ester Synthesis13m
- Synthesis of Amino Acids: Strecker Synthesis13m
- Reactions of Amino Acids: Esterification7m
- Reactions of Amino Acids: Acylation3m
- Reactions of Amino Acids: Hydrogenolysis6m
- Reactions of Amino Acids: Ninhydrin Test11m
- 30. Peptides and Proteins2h 42m
- Peptides12m
- Primary Protein Structure4m
- Secondary Protein Structure17m
- Tertiary Protein Structure11m
- Disulfide Bonds17m
- Quaternary Protein Structure10m
- Summary of Protein Structure7m
- Intro to Peptide Sequencing2m
- Peptide Sequencing: Partial Hydrolysis25m
- Peptide Sequencing: Partial Hydrolysis with Cyanogen Bromide7m
- Peptide Sequencing: Edman Degradation28m
- Merrifield Solid-Phase Peptide Synthesis18m
- 31. Catalysis in Organic Reactions1h 30m
- 32. Lipids 2h 50m
- 33. The Organic Chemistry of Metabolic Pathways2h 52m
- Intro to Metabolism6m
- ATP and Energy6m
- Intro to Coenzymes3m
- Coenzymes in Metabolism16m
- Energy Production in Biochemical Pathways5m
- Intro to Glycolysis3m
- Catabolism of Carbohydrates: Glycolysis27m
- Glycolysis Summary15m
- Pyruvate Oxidation (Simplified)4m
- Anaerobic Respiration11m
- Catabolism of Fats: Glycerol Metabolism11m
- Intro to Citric Acid Cycle7m
- Structures of the Citric Acid Cycle19m
- The Citric Acid Cycle35m
- 34. Nucleic Acids1h 32m
- 35. Transition Metals6h 14m
- Electron Configuration of Elements45m
- Coordination Complexes20m
- Ligands24m
- Electron Counting10m
- The 18 and 16 Electron Rule13m
- Cross-Coupling General Reactions40m
- Heck Reaction40m
- Stille Reaction13m
- Suzuki Reaction25m
- Sonogashira Coupling Reaction17m
- Fukuyama Coupling Reaction15m
- Kumada Coupling Reaction13m
- Negishi Coupling Reaction16m
- Buchwald-Hartwig Amination Reaction19m
- Eglinton Reaction17m
- Catalytic Allylic Alkylation18m
- Alkene Metathesis23m
- 36. Synthetic Polymers1h 49m
- Introduction to Polymers6m
- Chain-Growth Polymers10m
- Radical Polymerization15m
- Cationic Polymerization8m
- Anionic Polymerization8m
- Polymer Stereochemistry3m
- Ziegler-Natta Polymerization4m
- Copolymers6m
- Step-Growth Polymers11m
- Step-Growth Polymers: Urethane6m
- Step-Growth Polymers: Polyurethane Mechanism10m
- Step-Growth Polymers: Epoxy Resin8m
- Polymers Structure and Properties8m
A-Values: Study with Video Lessons, Practice Problems & Examples
 Created using AI
Created using AITo calculate the percentages of cyclohexane conformations using Gibbs free energy, apply the equation ΔG = -RT ln(KE). Here, R is the gas constant (8.314 J/mol·K) and T is temperature in Kelvin. The equilibrium constant (KE) is derived from the ratio of products to reactants, indicating favored conformations. A KE greater than 1 suggests a preference for equatorial over axial conformations. The final percentage of equatorial conformations can be calculated as x = KE / (KE + 1) × 100, where x represents the favored conformation.
Now that we know how to calculate the difference in flip energy, we can plug that information into the famous Equilibrium Constant equation to determine exact Ke of the reaction.
Calculating Chair Equilibrium
Video transcript
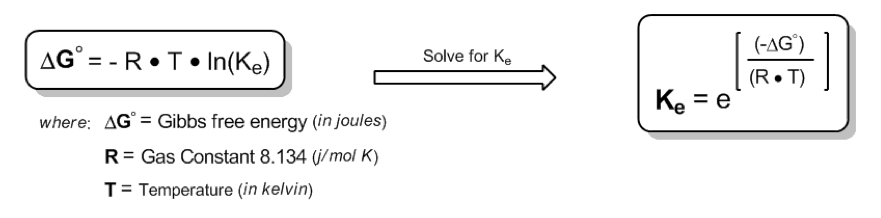
Gas Constant correct number:8.314
Once we have the Ke of the equilibria, we can solve for x, which will be the percentage of my most favored chair.
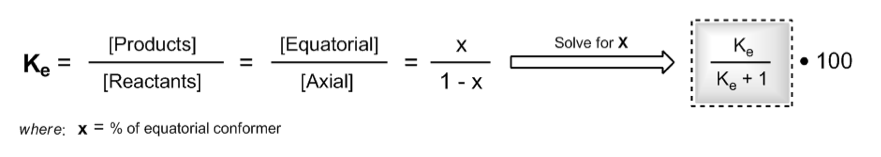
Estimate the equilibrium composition of the chair conformers of the following cyclohexanes at room temp:
cis-1,3-diethylcyclohexane
Problem Transcript
Did you remember to use the correct Gas Constant number?! (8.314)
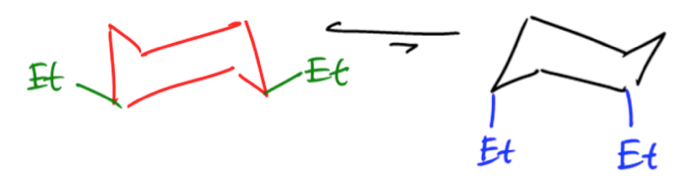
Estimate the equilibrium composition of the chair conformers of trans-1-methyl-3-phenylcyclohexane at room temperature.
Problem Transcript
Note: The correct value for methyl should be 7.6, not 4.2
With that, the correct answer should be closer to 88% / 12% for the percentage of both chairs using the correct value for R (8.314). Hope that makes sense!
Do you want more practice?
More setsHere’s what students ask on this topic:
What are A-values in organic chemistry?
A-values, or axial values, are numerical values that represent the free energy difference between axial and equatorial positions in cyclohexane conformations. These values help predict the stability of different substituents in cyclohexane rings. A higher A-value indicates a greater preference for the equatorial position due to steric hindrance in the axial position. Understanding A-values is crucial for determining the most stable conformation of substituted cyclohexanes.
 Created using AI
Created using AIHow do you calculate the percentage of equatorial and axial conformations in cyclohexane?
To calculate the percentage of equatorial and axial conformations in cyclohexane, use the Gibbs free energy equation: . Here, is the gas constant (8.314 J/mol·K) and is the temperature in Kelvin. The equilibrium constant is derived from the ratio of products to reactants. The percentage of equatorial conformations is calculated as .
 Created using AI
Created using AIWhy is the equatorial position more stable than the axial position in cyclohexane?
The equatorial position in cyclohexane is more stable than the axial position due to reduced steric hindrance. In the axial position, substituents experience 1,3-diaxial interactions with hydrogen atoms on the same side of the ring, leading to increased steric strain. In contrast, the equatorial position allows substituents to be more spread out, minimizing these interactions and resulting in a more stable conformation.
 Created using AI
Created using AIHow does temperature affect the equilibrium between axial and equatorial conformations in cyclohexane?
Temperature affects the equilibrium between axial and equatorial conformations in cyclohexane by influencing the Gibbs free energy change (ΔG). As temperature increases, the equilibrium constant can shift, altering the ratio of equatorial to axial conformations. Higher temperatures generally increase the energy available to overcome steric hindrance, potentially leading to a higher proportion of axial conformations. However, the exact effect depends on the specific ΔG values for the substituents involved.
 Created using AI
Created using AIWhat is the significance of the Gibbs free energy equation in determining cyclohexane conformations?
The Gibbs free energy equation is significant in determining cyclohexane conformations because it allows for the calculation of the equilibrium constant , which indicates the ratio of equatorial to axial conformations. By knowing ΔG, which can be derived from A-values, and the temperature, one can determine the favored conformation and calculate the exact percentages of each conformation. This is crucial for understanding the stability and behavior of substituted cyclohexanes.
 Created using AI
Created using AIYour Organic Chemistry tutors
- Using the data obtained in Problem 85, calculate the amount of steric strain in each of the chair conformers o...
- Using the data obtained in Problem 81, calculate the percentage of molecules of trans-1,2-dimethylcyclohexane ...
- (••) The A value of a substituent on a cyclohexane ring is essentially the ∆G° for a substituent going from th...
- (••) The A value of a substituent on a cyclohexane ring is essentially the ∆G° for a substituent going from th...
- (••) The A value of a substituent on a cyclohexane ring is essentially the ∆G° for a substituent going from th...
- The ∆G° for conversion of “axial” fluorocyclohexane to “equatorial” fluorocyclohexane at 25 °C is -0.25kcal>...
- b. Why is the percentage of molecules with the substituent in an equatorial position greater forisopropylcyclo...
- (••) The A value of a substituent on a cyclohexane ring is essentially the ∆G° for a substituent going from th...
- Using the data in Table 3.9, calculate the percentage of molecules of cyclohexanol that have the OH group in a...

